Unveiling the Riemann Zeta Function Through Integer Lattice Points 🔍

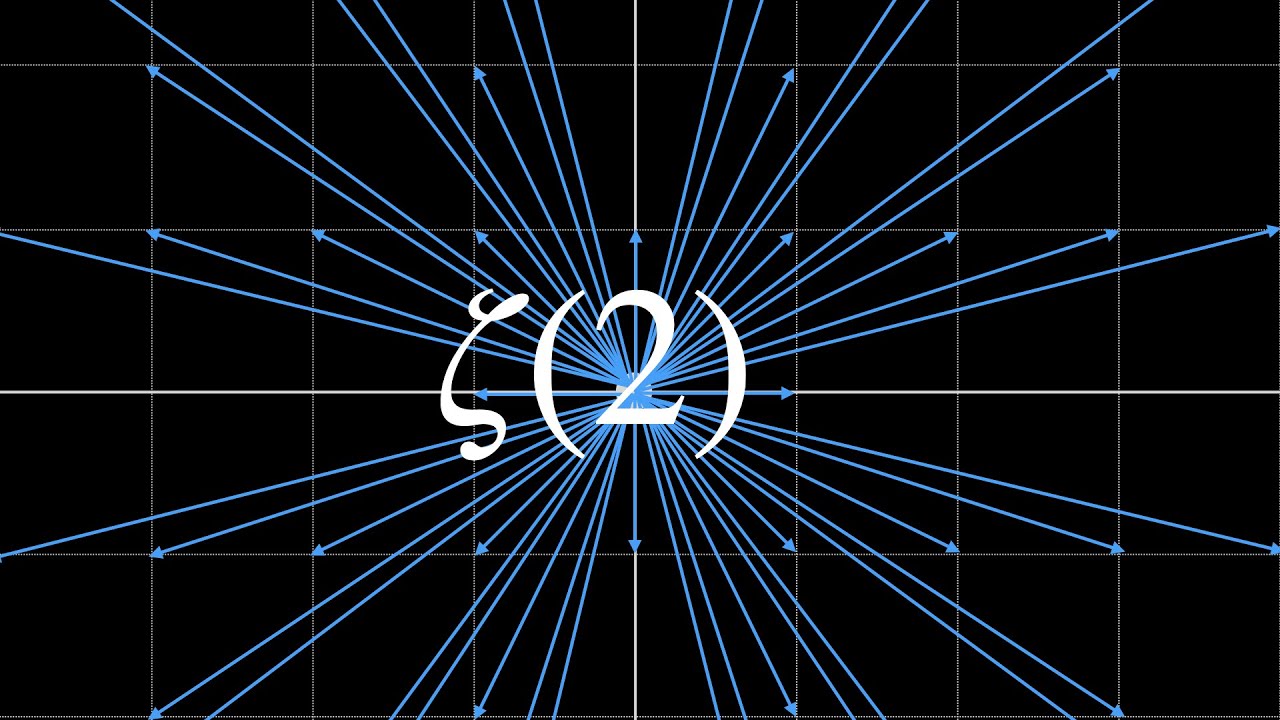
In this video we discuss visible points on the integer lattice and it's connection to the Riemann zeta function.

Sources:
1. The main derivation was based on the blog post
https://shreevatsa.wordpress.com/2008/11/07/lattice-points-visible-from-the-origin/

2. A slightly more formal version of the argument given above for the probability of two integers being coprime is given in the introduction in:
https://hal.archives-ouvertes.fr/hal-01413829/document.

3. A formal proof of the equivalence of coprime integers and visible points is given in Theorem 2.13 of:
https://documents.kenyon.edu/math/GarbettJSenEx2011.pdf

4. A the proof of the relation between coprime integers and the zeta function is given in "An introduction to the theory of numbers" by Hardy and Wright (4th edition). (See "Quadratfrei" numbers).

FAQ : How do you make these animations?
Animations are mostly made in Apple Keynote which has lots of functionality for animating shapes, lines, curves and text (as well as really good LaTeX). For some of the more complex animations, I use the Manim library. Editing and voiceover work in DaVinci Resolve.