Unveiling Euler’s Pi Prime Product & Riemann’s Zeta Function 🔍
Discover two fascinating mathematical concepts—Euler’s Pi Prime Product and Riemann’s Zeta Function—in this insightful video. Support Mathologer on Patreon or PayPal to explore more math mysteries!
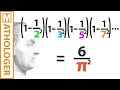
Mathologer
408.6K views • Sep 8, 2017
About this video
NEW (Christmas 2019). Two ways to support Mathologer
Mathologer Patreon: https://www.patreon.com/mathologer
Mathologer PayPal: paypal.me/mathologer
(see the Patreon page for details)
What has pi to do with the prime numbers, how can you calculate pi from the licence plate numbers you encounter on your way to work, and what does all this have to do with Riemann's zeta function and the most important unsolved problem in math? Well, Euler knew most of the answers, long before Riemann was born.
I got this week's pi t-shirt from here: https://shirt.woot.com/offers/beautiful-pi
As usual thank you very much to Marty and Danil for their feedback on an earlier version of this video and Michael (Franklin) for his help with recording this video..
Here are a few interesting references to check out if you can handle more maths: J.E. Nymann, On the probability that k positive integers are relatively prime, Journal of number theory 4, 469--473 (1972) http://www.sciencedirect.com/science/article/pii/0022314X72900388 (contains a link to a pdf file of the article).
Enjoy :)
Mathologer Patreon: https://www.patreon.com/mathologer
Mathologer PayPal: paypal.me/mathologer
(see the Patreon page for details)
What has pi to do with the prime numbers, how can you calculate pi from the licence plate numbers you encounter on your way to work, and what does all this have to do with Riemann's zeta function and the most important unsolved problem in math? Well, Euler knew most of the answers, long before Riemann was born.
I got this week's pi t-shirt from here: https://shirt.woot.com/offers/beautiful-pi
As usual thank you very much to Marty and Danil for their feedback on an earlier version of this video and Michael (Franklin) for his help with recording this video..
Here are a few interesting references to check out if you can handle more maths: J.E. Nymann, On the probability that k positive integers are relatively prime, Journal of number theory 4, 469--473 (1972) http://www.sciencedirect.com/science/article/pii/0022314X72900388 (contains a link to a pdf file of the article).
Enjoy :)
Tags and Topics
Browse our collection to discover more content in these categories.
Video Information
Views
408.6K
Likes
11.0K
Duration
15:23
Published
Sep 8, 2017
User Reviews
4.8
(81) Related Trending Topics
LIVE TRENDSRelated trending topics. Click any trend to explore more videos.
Trending Now