Unraveling the Average-Case Complexity of Tensor Decomposition 🧩

Computer Science/Discrete Mathematics Seminar I

Topic: Average-Case Computational Complexity of Tensor Decomposition
Speaker: Alex Wein
Affiliation: University of California, Davis
Date: October 24, 2022

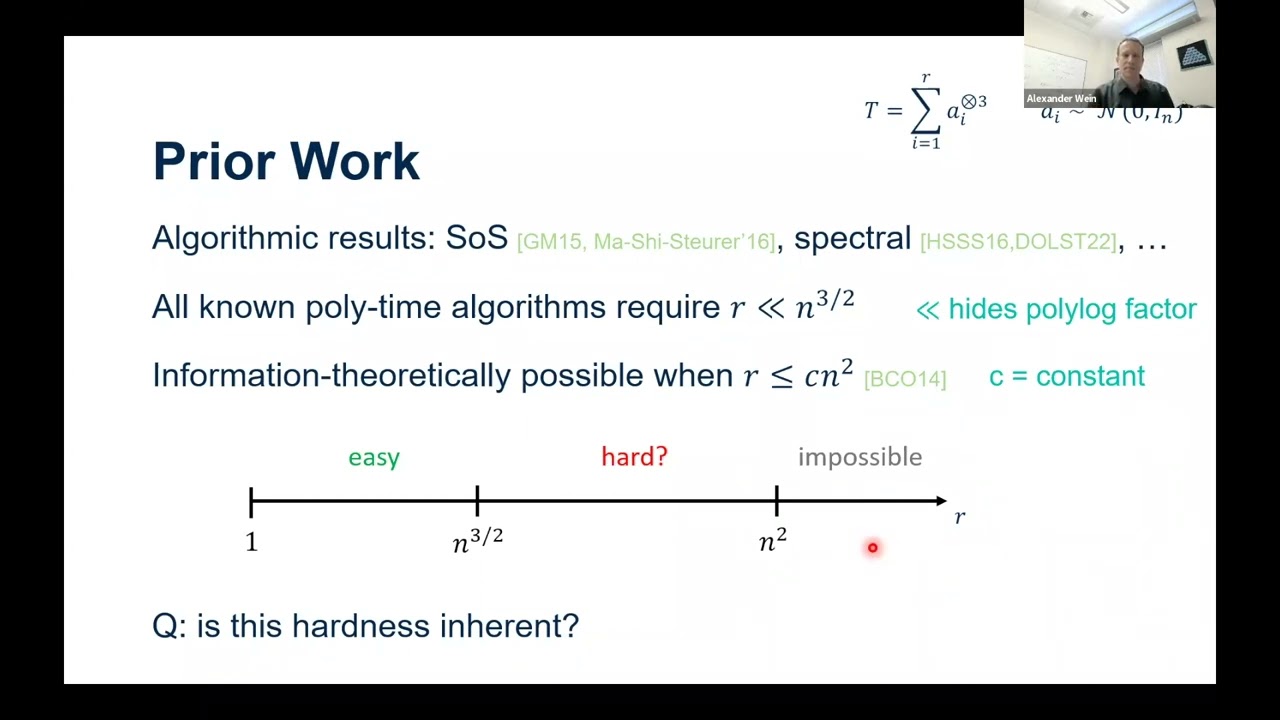
Suppose we are given a random rank-r order-3 tensor---that is, an n-by-n-by-n array of numbers that is the sum of r random rank-1 terms---and our goal is to recover the individual rank-1 terms. In principle this decomposition task is possible when rcn2 for a constant c, but all known poly-time algorithms require rn3/2. Is this a fundamental barrier for efficient algorithms?

In recent years, the average-case complexity of various high-dimensional statistical tasks has been resolved in restricted-but-powerful models of computation such as statistical queries, sum-of-squares, or low-degree polynomials. However, the hardness of tensor decomposition has remained elusive, and I will explain what makes this problem difficult. We show the first formal hardness for average-case tensor decomposition: when rn3/2, the decomposition task is hard for algorithms that can be expressed as low-degree polynomials in the tensor entries.

Wein-2022-10-24