Turing Machine as an Adder: Single Tape Addition Techniques

Welcome to Smart But Clever! In this session, we treat the Turing Machine as an adder—a transducer that reads two numbers and outputs their sum on the tape. We build a single-tape deterministic TM that performs binary addition, perfect for Automata Theory / TOC learners and GATE/UGC NET aspirants.

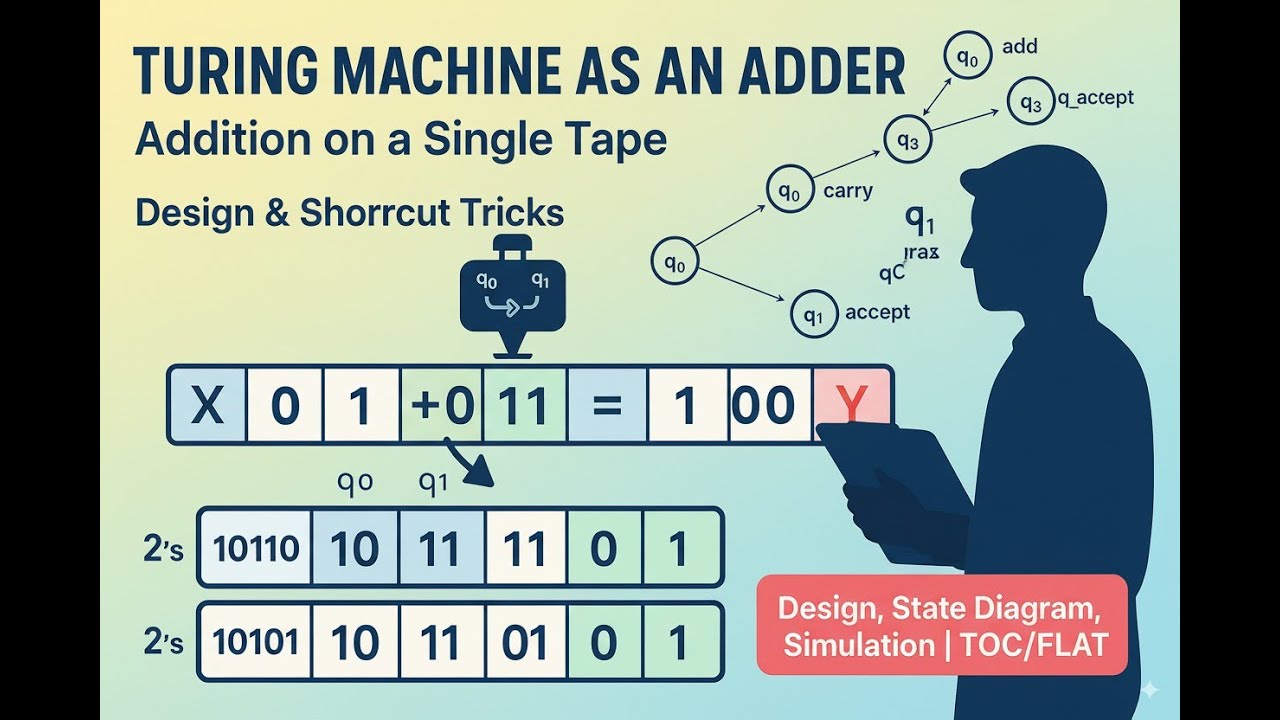
We formalize the input as x#y (two numbers separated by ‘0’) and design the TM to produce x + y in place (overwriting the second operand and erasing the first/0). The core idea is right-to-left addition with carry encoded in states: move to the right end, add corresponding bits of x and y, write the result in y’s cell, propagate carry, and continue past the ‘#’ boundary as needed. If both numbers end while carry=1, we extend the tape with a new leading 1. We cover the state/transition patterns, a clear hand simulation on sample inputs, edge cases (different lengths, all-ones plus one, leading zeros), and a brief complexity note (linear passes with careful head movement). You’ll also get shortcut tricks: treat blank as 0, encode carry in the control, and clean up leading zeros last.

What you’ll learn:

TM as a transducer for arithmetic (input/output conventions)
Binary addition with carry states (c=0/c=1) on a single tape
Input format x#y and in-place output strategy
Reusable state diagram/transition templates for adders
Worked simulations and edge cases (unequal lengths, overflow)
Shortcut tricks to minimize scans and states
Correctness invariants and quick time/space notes

If this helped, subscribe to Smart But Clever for more Automata, Compilers, and Algorithms. Like, share, and drop your doubts in the comments!

Prerequisites: Basic TM model (tape alphabet, blank, L/R moves), reading TM state diagrams.