Ben Lee Volk Unveils New Lower Bounds in Algebraic Complexity Theory 📊

Monday Apr 26, 2021
Recent lower bounds in algebraic complexity theory
(Ben Lee Volk, University of Texas at Austin)

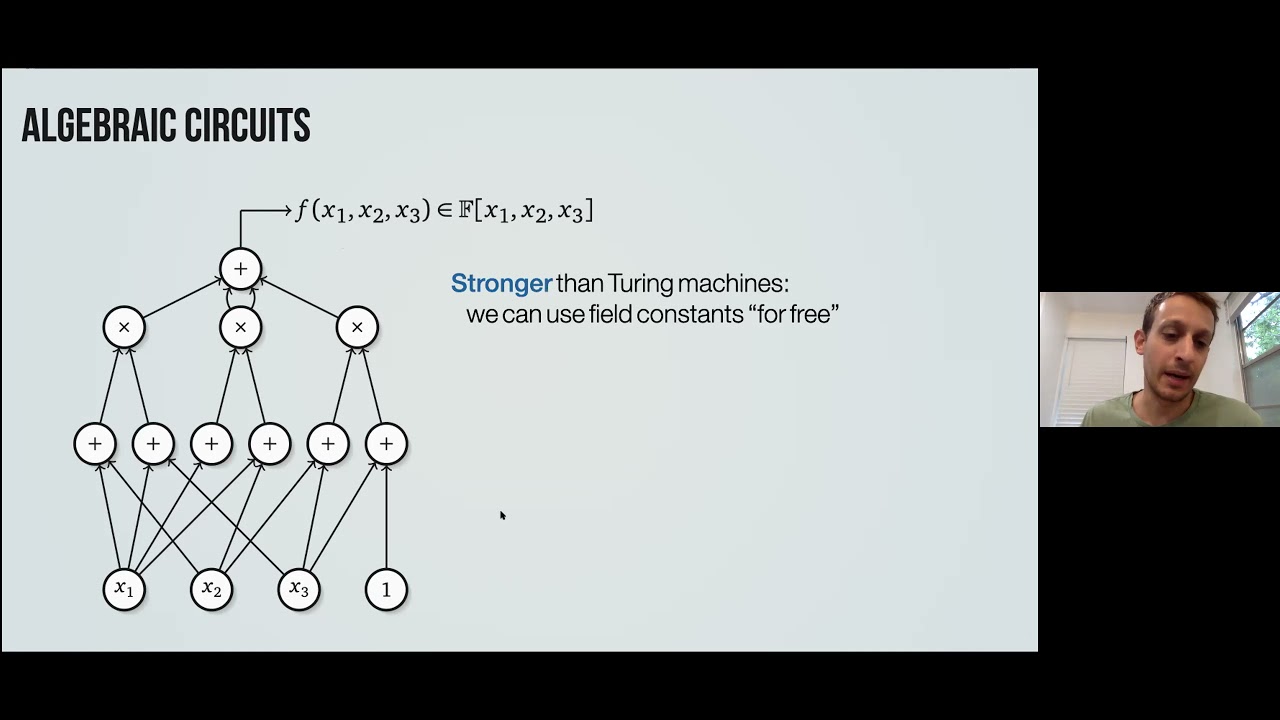
Algebraic complexity theory studies the complexity of solving algebraic computational tasks using algebraic models of computation. One major problem in this area is to prove lower bounds on the number of arithmetic operations required for computing explicit polynomials. This natural mathematical problem is the algebraic analog of the famous P vs. NP problem. It also has tight connections to other classical mathematical areas and to fundamental questions in complexity theory.

In this talk I will provide background and then present some recent progress on proving lower bounds for models of algebraic computation, such as the algebraic analogs of NC^1 and NL.

Based on joint works with Prerona Chatterjee, Mrinal Kumar and Adrian She.