Unraveling Albertson's Conjecture: A Challenging Puzzle in Graph Theory 🔍

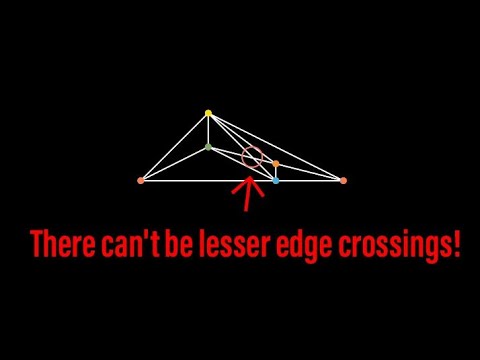
Albertson's conjecture says that the crossing number of a graph with chromatic number r, is always greater than or equal to the minimum crossing number of a complete graph. Although has been verified upto r=18, it still remains as an open problem. Credits: Wikipedia: https://en.m.wikipedia.org/wiki/Albertson_conjecture Related works: https://www.ijsr.net/archive/v4i5/SUB154344.pdf Proof for r less than or equal to 12: https://arxiv.org/pdf/1006.3783 Work on r less than or equal to 16: https://arxiv.org/pdf/0909.0413 Remarks on the last paper: https://www.combinatorics.org/ojs/index.php/eljc/article/view/v21i1p57/pdf For r less than or equal to 18: https://arxiv.org/pdf/1509.01932 Music: Mozart: Andante from Piano Concerto no. 21 KV 467  Code: https://github.com/ishanbaner/Manim-codes/blob/main/Albertson.py