Unlocking RSA Security: A Key Fact About Factoring in Abstract Algebra 🔐
Discover a crucial algebraic property that relates to factoring integers and how it impacts the RSA cryptography algorithm. Perfect for math enthusiasts and cybersecurity buffs!

Henry Adams
171 views • Mar 14, 2021
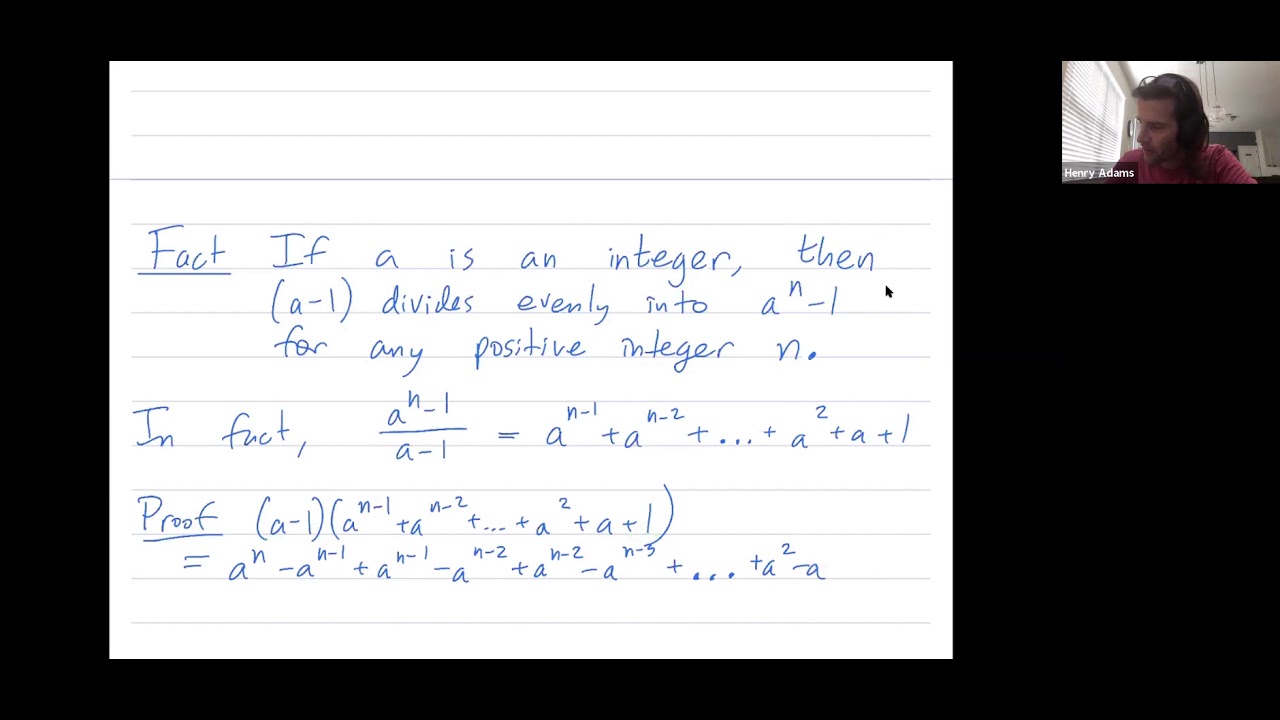
About this video
Abstract Algebra 44: A factoring fact related to the RSA cryptography algorithm
Abstract: If a is an integer that is at least 2, then a-1 divides evenly into a^n-1 for any positive integer n. We give an explanation of this factoring fact. We will later use this fact when giving a partial explanation of why the RSA public key cryptography system works.
This video accompanies the class "Introduction to Abstract Algebra" at Colorado State University:
https://www.math.colostate.edu/~adams/teaching/math366spr2021/
Abstract: If a is an integer that is at least 2, then a-1 divides evenly into a^n-1 for any positive integer n. We give an explanation of this factoring fact. We will later use this fact when giving a partial explanation of why the RSA public key cryptography system works.
This video accompanies the class "Introduction to Abstract Algebra" at Colorado State University:
https://www.math.colostate.edu/~adams/teaching/math366spr2021/
Video Information
Views
171
Likes
4
Duration
5:23
Published
Mar 14, 2021
Related Trending Topics
LIVE TRENDSRelated trending topics. Click any trend to explore more videos.