Unlocking Chaos: Bifurcation Analysis of the Logistic Map 🌟

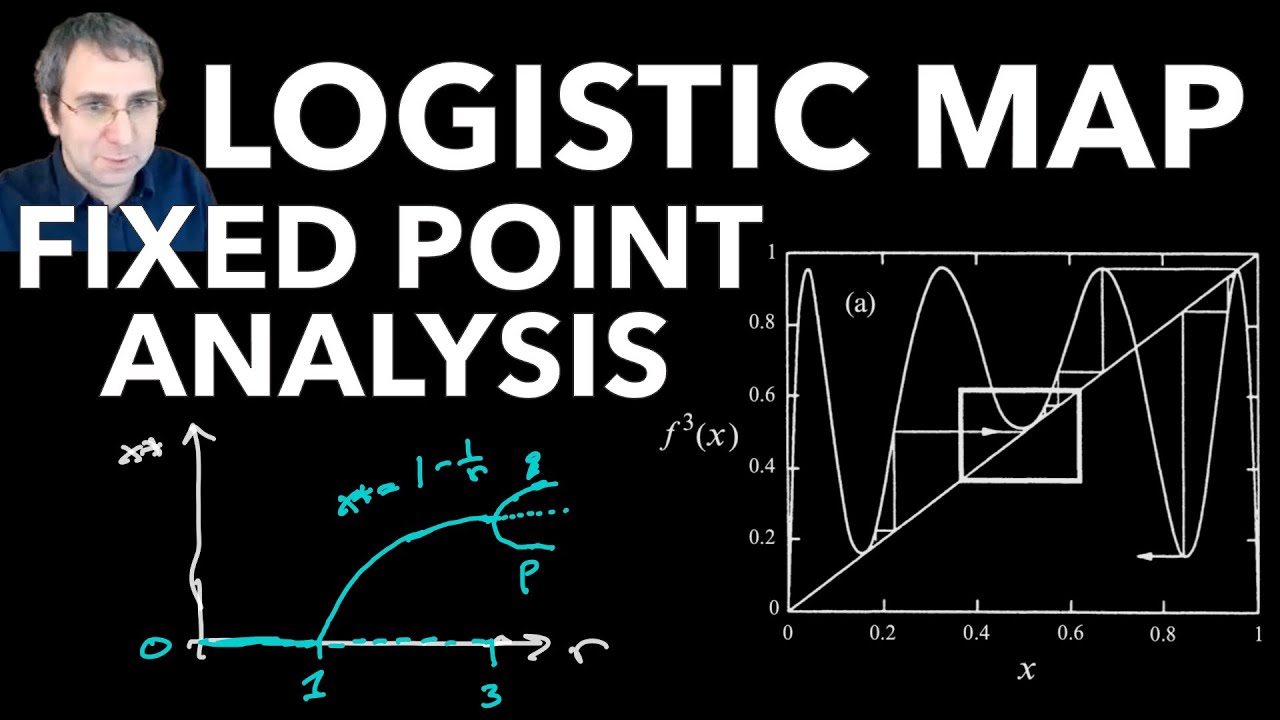
The logistic map bifurcation diagram can be analytically explained. We calculate the value of first few bifurcation points, where the non-zero fixed point emerges and stable cycles of period 2 and 4 emerge via a period-doubling bifurcation (or flip bifurcation). We see a map version of fixed point ghosts and bottlenecks, regions of high residence time, related to the intermittency route to chaos.

► Next, the universality of features in the logistic map
https://youtu.be/PM6fSdhcw4M

► Logistic map
Introduction https://youtu.be/PVo1mHnU7WU
Bifurcation diagram https://youtu.be/2nEBSyMsQE8

► Additional background
Introduction to mappings https://youtu.be/-vV5A4HullY
Logistic equation (1D ODE) https://youtu.be/iOumaIR5gzA
Lorenz map on strange attractor https://youtu.be/P4tjxOFnGNo
Lorenz equations introduction https://youtu.be/fIG2jtOhW0U
Definitions of chaos and attractor https://youtu.be/uDpYU01dhk0

► Ghosts and bottlenecks
In 1D differential equations https://youtu.be/Q_0oB1DHyQU
In 2D differential equations https://youtu.be/pl3byZQkVd8

► From 'Nonlinear Dynamics and Chaos' (online course).
Playlist https://is.gd/NonlinearDynamics

► Dr. Shane Ross, Virginia Tech professor (Caltech PhD)
Subscribe https://is.gd/RossLabSubscribe​

► Follow me on Twitter
https://twitter.com/RossDynamicsLab

► Course lecture notes (PDF)
https://is.gd/NonlinearDynamicsNotes

► Advanced lecture on maps from another of my courses
https://youtu.be/NYoA5B2qsdc

► Robert May's 1976 article introducing the logistic map (PDF)
https://is.gd/logisticmappaper

► Courses and Playlists by Dr. Ross

📚Attitude Dynamics and Control
https://is.gd/SpaceVehicleDynamics

📚Nonlinear Dynamics and Chaos
https://is.gd/NonlinearDynamics

📚Hamiltonian Dynamics
https://is.gd/AdvancedDynamics

📚Three-Body Problem Orbital Mechanics
https://is.gd/SpaceManifolds

📚Lagrangian and 3D Rigid Body Dynamics
https://is.gd/AnalyticalDynamics

📚Center Manifolds, Normal Forms, and Bifurcations
https://is.gd/CenterManifolds


References:
Steven Strogatz, "Nonlinear Dynamics and Chaos", Chapter 10: One-Dimensional Maps






intermittent period doubling cascade period-doubling bifurcation flip bifurcation discrete map analog of logistic equation Poincare map largest Liapunov exponent fractal dimension of lorenz attractor box-counting dimension crumpled paper stable focus unstable focus supercritical subcritical topological equivalence genetic switch structural stability Andronov-Hopf Andronov-Poincare-Hopf small epsilon method of multiple scales two-timing Van der Pol Oscillator Duffing oscillator nonlinear oscillators nonlinear oscillation nerve cells driven current nonlinear circuit glycolysis biological chemical oscillation Liapunov gradient systems Conley index theory gradient system autonomous on the plane phase plane are introduced 2D ordinary differential equations cylinder bifurcation robustness fragility cusp unfolding perturbations structural stability emergence critical point critical slowing down supercritical bifurcation subcritical bifurcations buckling beam model change of stability nonlinear dynamics dynamical systems differential equations dimensions phase space Poincare Strogatz graphical method Fixed Point Equilibrium Equilibria Stability Stable Point Unstable Point Linear Stability Analysis Vector Field Two-Dimensional 2-dimensional Functions Hamiltonian Hamilton streamlines weather vortex dynamics point vortices topology Verhulst Oscillators Synchrony Torus friends on track roller racer dynamics on torus Lorenz equations chaotic strange attractor convection chaos chaotic

#NonlinearDynamics #DynamicalSystems #Bifurcation #LogisticMap #PeriodDoubling #DifferenceEquation #PoincareMap #chaos #LorenzAttractor #LyapunovExponent #Lyapunov #Liapunov #Oscillators #Synchrony #Torus #Hopf #HopfBifurcation #NonlinearOscillators #AveragingTheory #LimitCycle #Oscillations #nullclines #RelaxationOscillations #VanDerPol #VanDerPolOscillator #LimitCycles #VectorFields #topology #geometry #IndexTheory #EnergyConservation #Hamiltonian #Streamfunction #Streamlines #Vortex #SkewGradient #Gradient #PopulationBiology #FixedPoint #DifferentialEquations #SaddleNode #Eigenvalues #HyperbolicPoints #NonHyperbolicPoint #CuspBifurcation #CriticalPoint #buckling #PitchforkBifurcation #robust #StructuralStability #DifferentialEquations #dynamics #dimensions #PhaseSpace #PhasePortrait #PhasePlane #Poincare #Strogatz #Wiggins #Lorenz #VectorField #GraphicalMethod #FixedPoints #EquilibriumPoints #Stability #NonlinearODEs #StablePoint #UnstablePoint #Stability #LinearStability #LinearStabilityAnalysis #StabilityAnalysis #VectorField #TwoDimensional #Functions #PopulationGrowth #PopulationDynamics #Population #Logistic #GradientSystem #GradientVectorField #Cylinder #Pendulum #Newton #LawOfMotion #dynamics #Poincare​ #mathematicians #maths #mathsmemes #math4life #mathstudents #mathematician #mathfacts #mathskills #mathtricks #KAMtori #Hamiltonian