Understanding the Traveling Salesman Problem Through Brute Force Animation

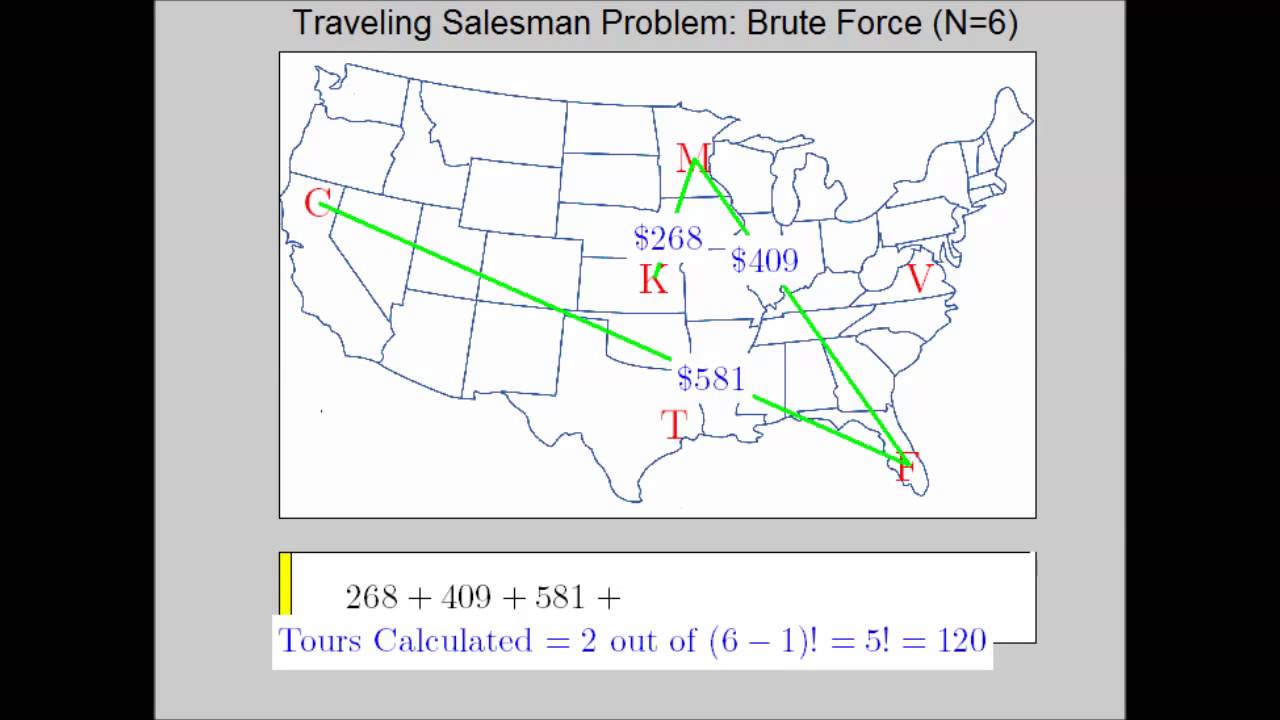
This animation, created using MATLAB, illustrates how the brute force algorithm is implemented to solve the traveling salesman problem, or TSP.

The TSP is a rather famous math problem intending to determine the cheapest way to travel (round-trip) to N different cities (or sites). Each round trip covering all the cities is called a tour. For N different cities for which to travel, there are (N-1)! different tours. These tours however, include reversals. For example, ABCDA (for 4 cities) is an equivalent tour to ADCBA. This means one only needs to check the distinct (N-1)!/2 tours. In this video, all (N-1)! tours are shown (since the permutations of the N cities are not generated in a particular order for which to easily select the distinct ones).

The Brute Force algorithm is accurate since we can guarantee the optimal (cheapest) tour. However, it is not efficient. Many TSP's involve more sites which makes the brute force algorithm work extremely hard. For example, for only 12 sites, there are 11! tours, which is almost 40 million tours. For only 30 cities, there are more tours than there are stars in the known universe.

More efficient algorithms like the Nearest Neighbor or Cheapest Link algorithm are more efficient. Their downside is the possible loss of accuracy.