Understanding Randomized Primality Testing with Fermat-Euler Theorem 🔍

Discover how finite group theory and the Fermat-Euler theorem improve primality testing algorithms. Learn why strict subgroups are limited to half the size of the group in this insightful explanation.

Understanding Randomized Primality Testing with Fermat-Euler Theorem 🔍
DG
27 views • Jan 14, 2021
Understanding Randomized Primality Testing with Fermat-Euler Theorem 🔍

About this video

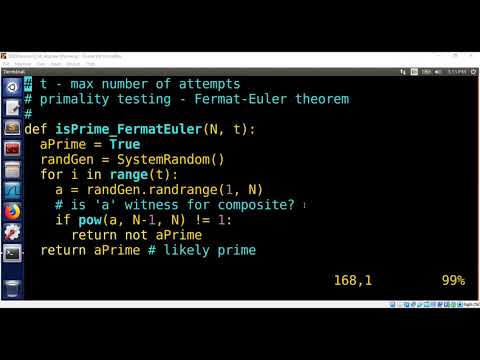
Let G be a finite group. We show that any strict subgroup of G can have at most |G|/2 elements.

This theorem is needed to analyze the primality testing algorithm (Fermat-Euler).

Tags and Topics

Browse our collection to discover more content in these categories.

#Size of a subgroup #finite group #number theory #group theory #primality testing

Video Information

Views

27

Duration

13:22

Published

Jan 14, 2021

Related Trending Topics

LIVE TRENDS

Related trending topics. Click any trend to explore more videos.

Trending Now
gonzaga basketball
1.0K+
high potential
2.0K+
v. j. edgecombe
500+
flyers vs canucks
1.0K+