Understanding How SHA-256 Works

An explanation of how SHA-256 works, with animations of the operations used inside the hash function.

I'm not a cryptographer though, so I can't explain the reasons behind the design (at the moment).

00:00 - Introduction
↳ 02:20 - Bitcoin Mining
05:05 - Basic Operations
08:27 - Functions
10:58 - Constants
12:23 - Hash Computation
↳ 12:41 - Message
↳ 13:19 - Padding
↳ 14:24 - Message Blocks
↳ 14:58 - Message Schedule
↳ 17:42 - Compression
↳ 22:30 - Final Hash Value

Source code for animations (and text guide): https://github.com/in3rsha/sha256-animation

Official specification: https://nvlpubs.nist.gov/nistpubs/FIPS/NIST.FIPS.180-4.pdf


====
FAQs:
====


=== What setup are you using for your computer? ===

* Operating System = Ubuntu (Xubuntu)
* Desktop Environment = XFCE
* Appearance Style = Arc-Dark
* Appearance Icons = Papirus-Dark
* Window Manager Style = Numix
* Wallpaper = A simple gradient from dark grey to grey.
* Shell = zsh (using zsh-autosuggestions)
* Terminal Font = Hack Regular


=== How do you work out the constants? ===

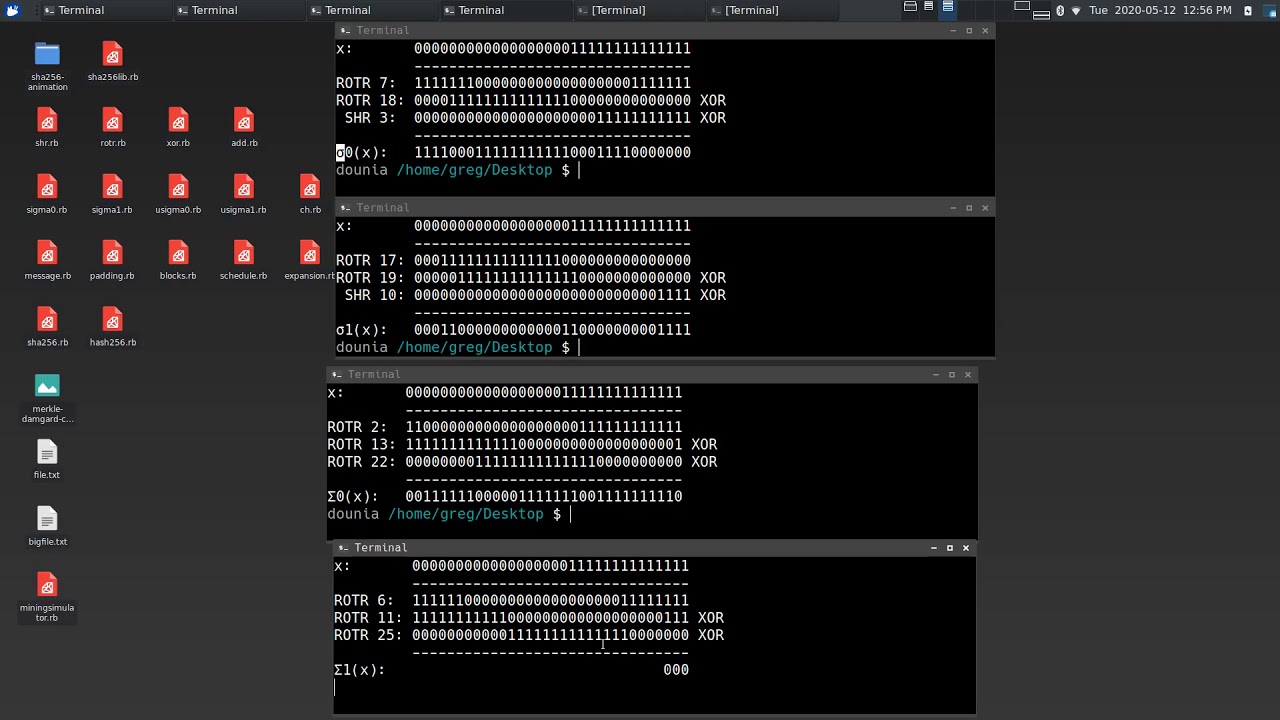
The constants are created using the first 32 bits from the fractional part of the cube roots of prime numbers.

For example, the first constant is the cube root of the first prime number (2), so:

∛2 = 1.2599210498948732

The fractional part of this is:

= 0.2599210498948732

However, we want 32 bits' worth of this fractional part. To get these 32 bits, we multiply the fraction by 2^32:

= 1116352408.8404646

The integer part of this is our 32-bit constant, which we can convert to binary:

= 1116352408
= 0b01000010100010100010111110011000

Here's some code showing how it works: https://github.com/in3rsha/sha256-animation/blob/master/constants.rb



=== How does the padding work if my message is X bits in length? ===

Lets say we have a message that is exactly 448 bits.

We always need to include the `1` separator and the 64 bit message size in the padding, which takes the message+padding up to 513 bits. This exceeds the 512 bit message block size we're after, so we pad with 511 zeros to take us up to 1024 bits (the next multiple of 512).

The zeros go between the separator and the size, like so:

[message] [separator] {zeros} [size]

So in other words, if your message and the initial padding takes you beyond the size of a message block, you pad all the way up to the next multiple of 512.