Understanding Divergence-Free Vector Fields as Curl of Another Field 🌐

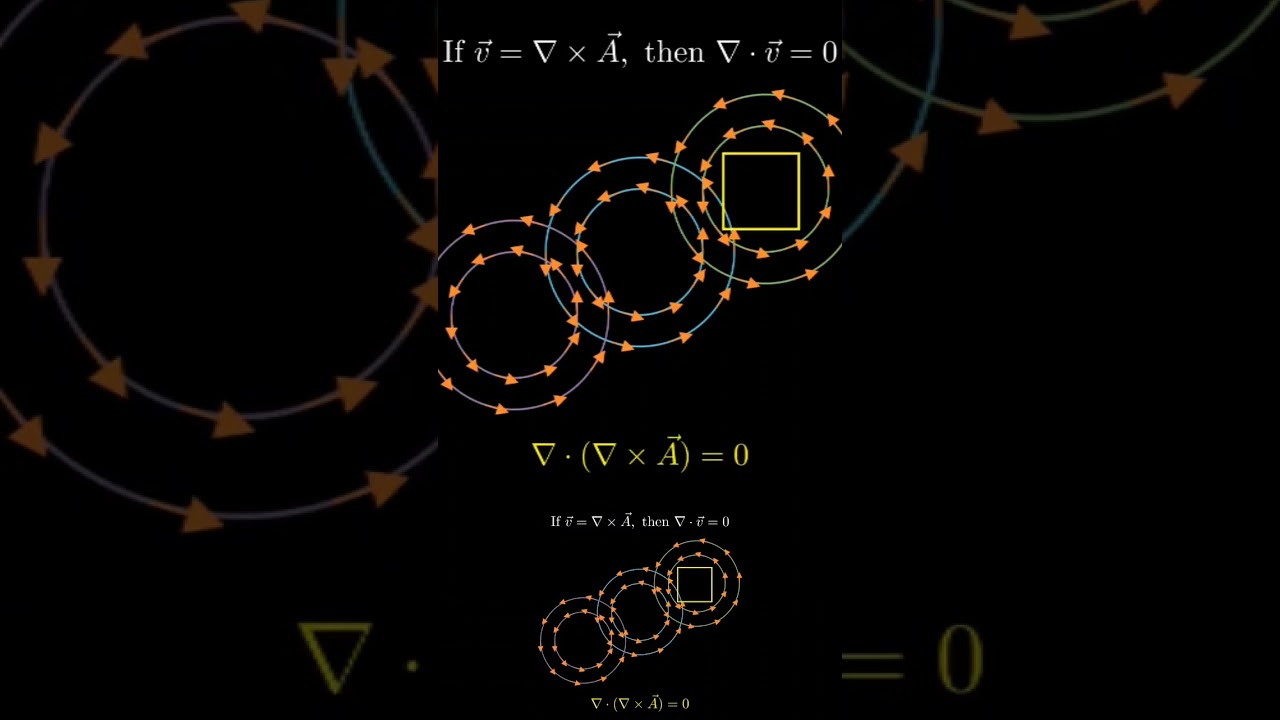
any vector field that can be expressed as the curl of another vector field must necessarily be divergence-free https://viadean.notion.site/Mathematical-Structures-Underlying-Physical-Laws-1ed1ae7b9a3280f78af4ecfe5b22c471 #maths #physics #python #vector #fields #caculus #potential #divergences #scalars #flux #density - The animation illustrates a fundamental theorem in vector calculus: if a vector field $\vec{v}$ is the curl of another vector field $\vec{A}$ (i.e., $\vec{v}=\nabla \times \vec{A}$ ), then its divergence is zero ( $\nabla \cdot \vec{v}=0$ ), a property visually represented by the circular flow patterns around a central square. - This concept, rooted in the Helmholtz decomposition, has practical implications in physics, such as in electromagnetism where magnetic fields (curl of a vector potential) are divergence-free, supported by Maxwell's equations and verified in experiments like those conducted by Faraday in the 1830s. - The image's depiction of divergence-free fields aligns with recent computational studies in fluid dynamics (e.g., peer-reviewed work in Journal of Computational Physics, 2023), showing how such fields model incompressible flows, challenging oversimplified educational narratives that overlook their real-world complexity.