Prim's Algorithm for Minimum Spanning Trees (MST) | Graph Theory

Support the production of this course by joining Wrath of Math to access all my graph theory videos!
https://www.youtube.com/channel/UCyEKvaxi8mt9FMc62MHcliw/join
🛍 Check out the coolest math clothes in the world: https://mathshion.com/

Graph Theory course: https://www.youtube.com/playlist?list=PLztBpqftvzxXBhbYxoaZJmnZF6AUQr1mH
Graph Theory exercises: https://www.youtube.com/playlist?list=PLztBpqftvzxXtYASoshtU3yEKqEmo1o1L

Get the textbook! https://amzn.to/3HvI535

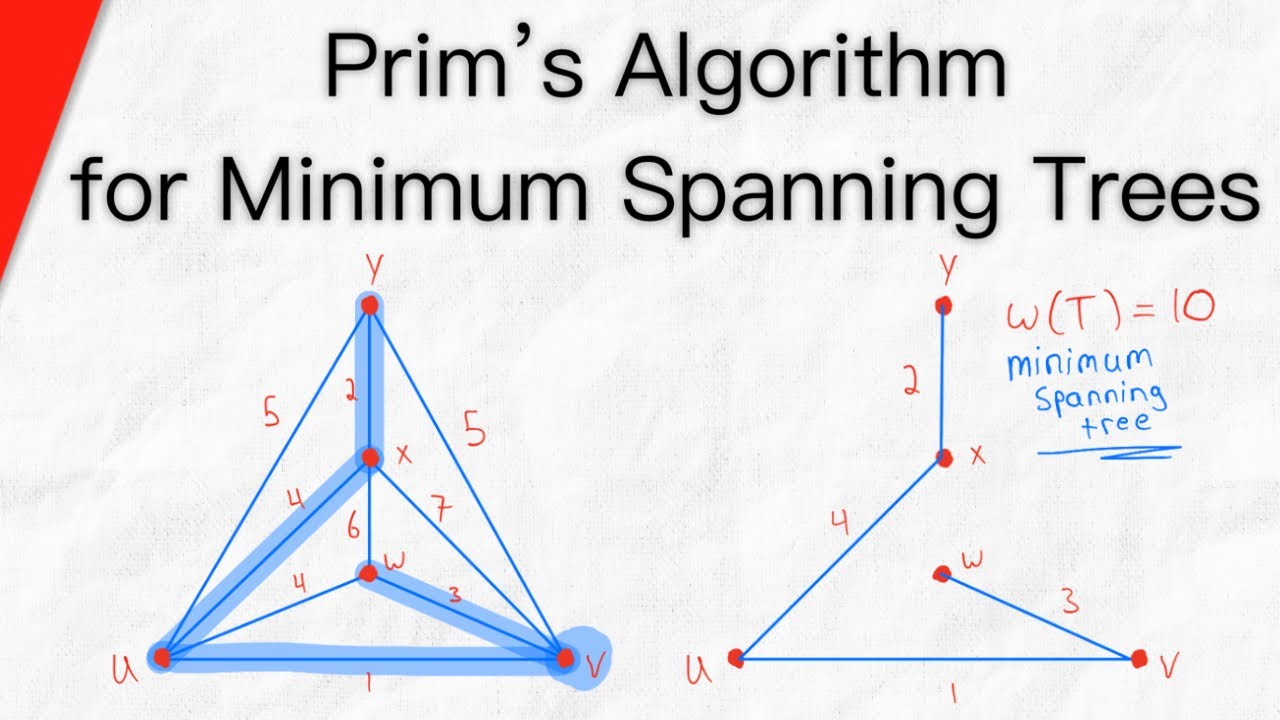
We go over Prim's Algorithm, and how it works to find minimum spanning trees (also called minimum weight spanning trees or minimum cost spanning trees). We'll also see two examples of using Prim's algorithm to find minimum spanning trees in connected weighted graphs.

This algorithm is one way to solve the problem of finding a spanning tree of minimum weight in a connected weighted graph. The weight of a subgraph of a weighted graph is the sum of the weights of the subgraph's edges. So, among all spanning trees of a graph G, if we use Prim's algorithm to find a minimum spanning tree T of G, it will be a spanning tree of minimum weight/minimum cost. Note that neither spanning trees nor minimum spanning trees are necessarily unique.

Spanning Subgraphs: https://youtu.be/Kh9LiX2farU
Proof Every Connected Graph has a Spanning Tree: https://youtu.be/-Ca_uP_wRp4
Kruskal's Algorithm for Minimum Spanning Trees: https://youtu.be/XFhW6vhvC64

★DONATE★
◆ Support Wrath of Math on Patreon for early access to new videos and other exclusive benefits: https://www.patreon.com/join/wrathofmathlessons
◆ Donate on PayPal: https://www.paypal.me/wrathofmath

Follow Wrath of Math on...
● Instagram: https://www.instagram.com/wrathofmathedu
● Facebook: https://www.facebook.com/WrathofMath
● Twitter: https://twitter.com/wrathofmathedu