Master Laplace Transforms for Differential Equations
Learn how Laplace transforms simplify solving second-order differential equations in this helpful tutorial. 🔧

Glythify
6.8K views • Jul 1, 2025
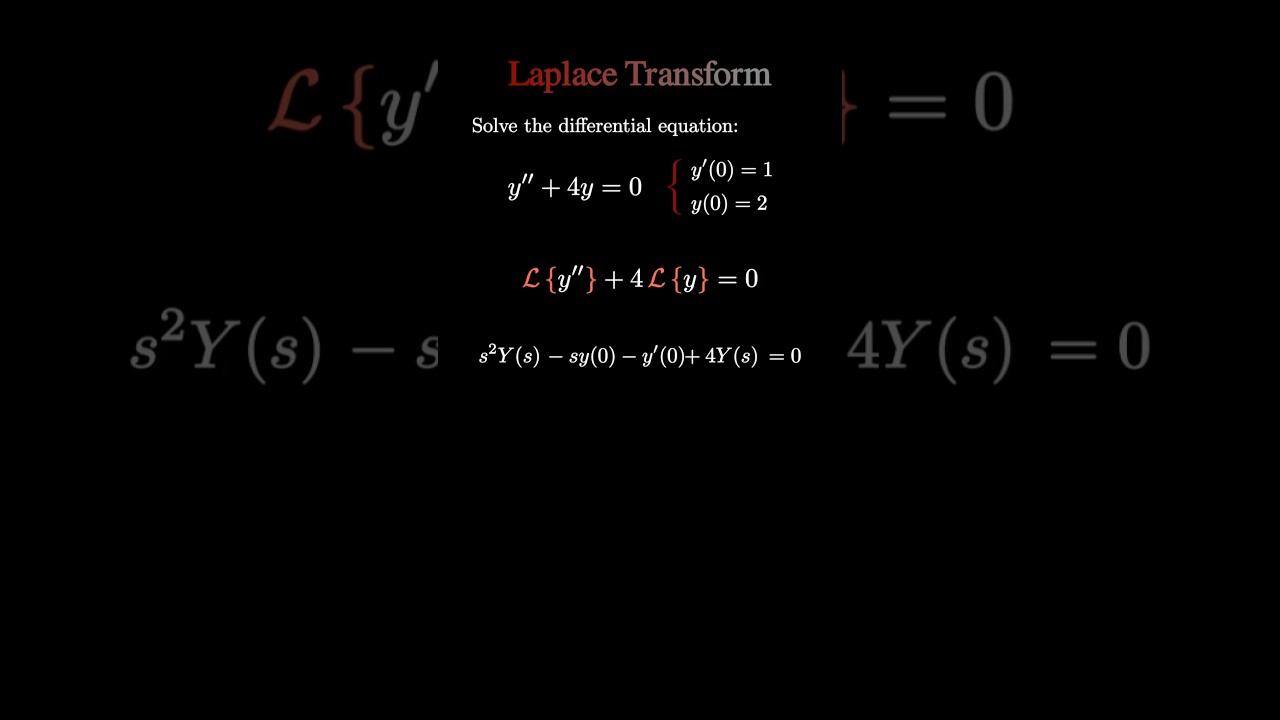
About this video
Struggling with differential equations? Let Laplace transforms save the day! 🔧📐
In this video, we solve the second-order linear differential equation y'' + 4y = 0 with initial conditions y'(0) = 1 and y(0) = 2 using the powerful Laplace transform method. We'll transform to the s-domain, solve algebraically, then transform back to get our final solution.
Why This Problem Matters:Laplace transforms are essential for engineering students and appear frequently in differential equations courses. This method converts challenging differential equations into simple algebraic problems. Many students get confused with initial conditions in the s-domain - we'll make it crystal clear!
What You'll Learn:
Apply Laplace transform to second-order derivatives
Handle initial conditions in the s-domain
Solve for Y(s) algebraically
Use inverse Laplace transforms to find y(t)
Verify solutions satisfy original equation and conditions
Key Concepts: Laplace transforms, inverse transforms, initial value problems, s-domain analysis, partial fractions
Comment below with YOUR toughest differential equation problem that you'd like me to solve in my next video!
In this video, we solve the second-order linear differential equation y'' + 4y = 0 with initial conditions y'(0) = 1 and y(0) = 2 using the powerful Laplace transform method. We'll transform to the s-domain, solve algebraically, then transform back to get our final solution.
Why This Problem Matters:Laplace transforms are essential for engineering students and appear frequently in differential equations courses. This method converts challenging differential equations into simple algebraic problems. Many students get confused with initial conditions in the s-domain - we'll make it crystal clear!
What You'll Learn:
Apply Laplace transform to second-order derivatives
Handle initial conditions in the s-domain
Solve for Y(s) algebraically
Use inverse Laplace transforms to find y(t)
Verify solutions satisfy original equation and conditions
Key Concepts: Laplace transforms, inverse transforms, initial value problems, s-domain analysis, partial fractions
Comment below with YOUR toughest differential equation problem that you'd like me to solve in my next video!
Video Information
Views
6.8K
Likes
128
Duration
0:23
Published
Jul 1, 2025
User Reviews
4.6
(1) Related Trending Topics
LIVE TRENDSRelated trending topics. Click any trend to explore more videos.
Trending Now