Master Circle Theorems in Just 3 Minutes! 🧠

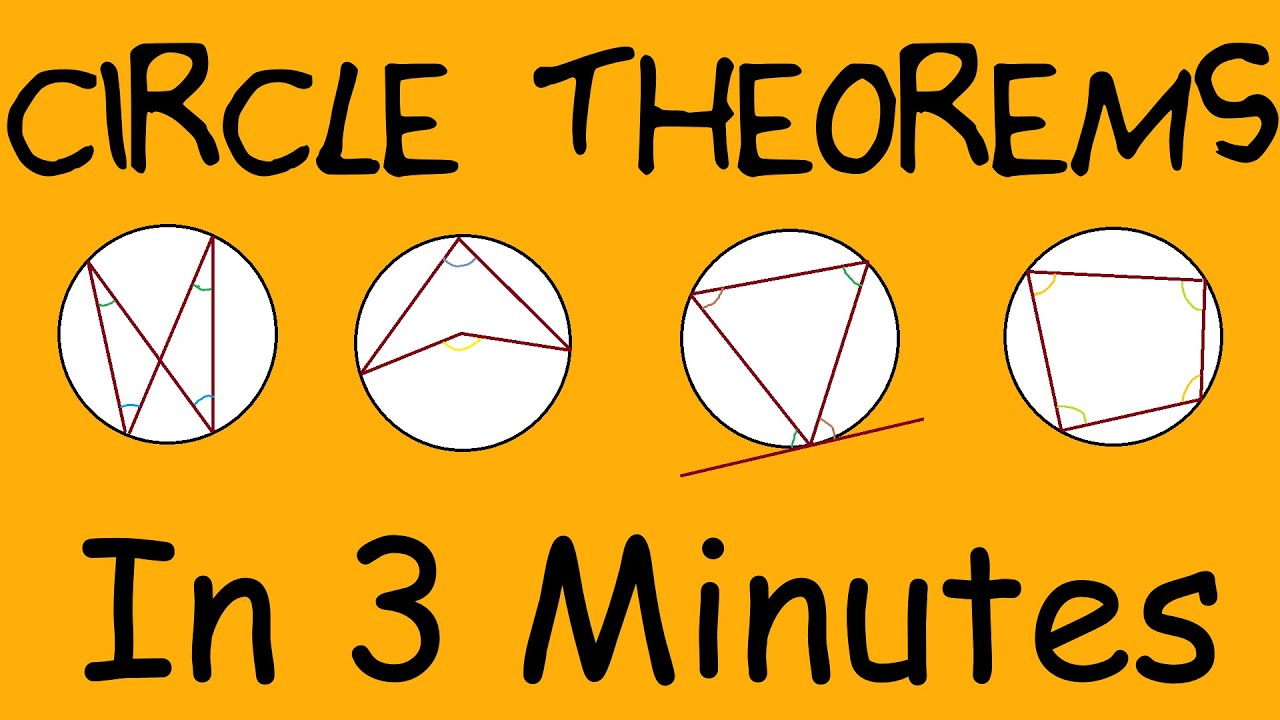
This is a graphic, simple and memorable way to remember the difference from a chord or a tangent or a segments and sectors! I made this after struggling to understand it myself, once i got to grips with it i decided to help others who were also stuck.. so this video was created...

This video includes Perpendicular bisectors of any chord
the angles in a semi-circle,
what happens when a tangent and a radius meet,
Angles that are in the same segment and how different they are, the circumference subtended by the same arc,
the meaning of subtended,
lengths of two tangents and finally the angle between a tangent and a chord.. aka Alternate Segment Theorem.

I re-uploaded this video because the last one had some glitches so here we are againn....


FOR THE QUESTION IF YOU ARE STUCK
okay so angle A is 55degrees. this is because the whole isosceles triangle adds up to 180degrees, you now take 70degrees from this because the angle on the far right hand side is 70degrees. this leaves us with 110degrees and you divide it by two (due to it being isosceles triangle) so angle A is 55degrees.

if you go to 1:07 this explains the next part on why there is a 90degree angle on top of angle B.
 you take 55degrees from that 90degrees because part of the right angle overlaps the first isosceles triangle (on the right hand side) and we have previously worked out that, that angle is 55degrees, this leaves us with 35degrees.

now times that 35 by 2 which gives you 70degrees, take that answer AWAY from 180degrees because as you can see angle D is within ANOTHER isosceles triangle which means all the angles within the triangle add up to 180degrees.

because angle D is within that triangle, angle D and the angle at the bottom right of the Isosceles triangle will EQUAL to the same amount.
now divide the 110degrees by 2 to give you 55degrees.