Key Facts About Orthogonal Polynomials

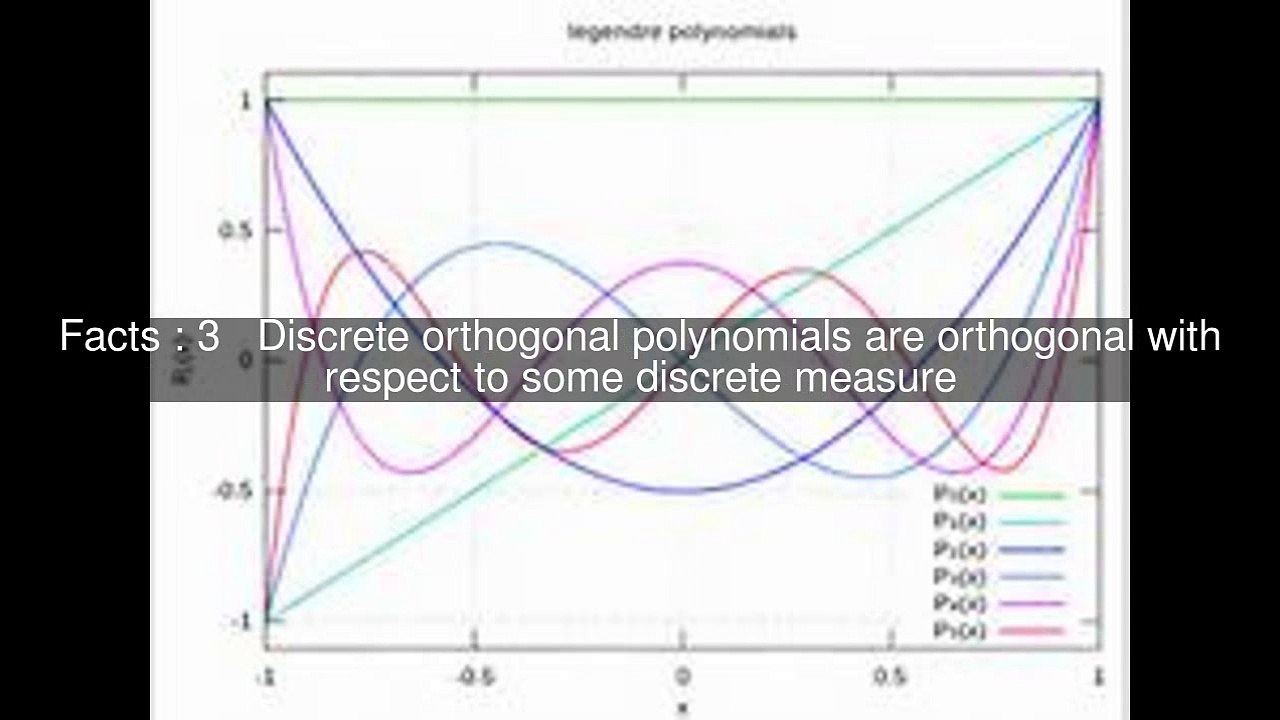
Facts : 1 Examples of orthogonal polynomials The most commonly used orthogonal polynomials are orthogonal for a measure with support in a real interval<br />Facts : 2 This includes: The classical orthogonal polynomials (Jacobi polynomials, Laguerre polynomials, Hermite polynomials, and their special cases Gegenbauer polynomials, Chebyshev polynomials and Legendre polynomials)<br />Facts : 3 Discrete orthogonal polynomials are orthogonal with respect to some discrete measure<br />Facts : 4 Sometimes the measure has finite support, in which case the family of orthogonal polynomials is finite, rather than an infinite sequence<br />Facts : 5 The Racah polynomials are examples of discrete orthogonal polynomials, and include as special cases the Hahn polynomials and dual Hahn polynomials, which in turn include as special cases the Meixner polynomials, Krawtchouk polynomials, and Charlier polynomials<br />Facts : 6 Sieved orthogonal polynomials, such as the sieved ultraspherical polynomials, sieved Jacobi polynomials, and sieved Pollaczek polynomials, have modified recurrence relations<br />Facts : 7 One can also consider orthogonal polynomials for some curve in the complex plane<br />Facts : 8 There are some families of orthogonal polynomials that are orthogonal on plane regions such as triangles or disks