Fourier Transform 22: Riemann–Lebesgue Lemma in Fourier Series
This video explores the Riemann–Lebesgue Lemma as it applies to Fourier Series, providing a detailed explanation and examples. For additional resources, visit the provided link.

The Bright Side of Mathematics
313 views • Nov 3, 2025
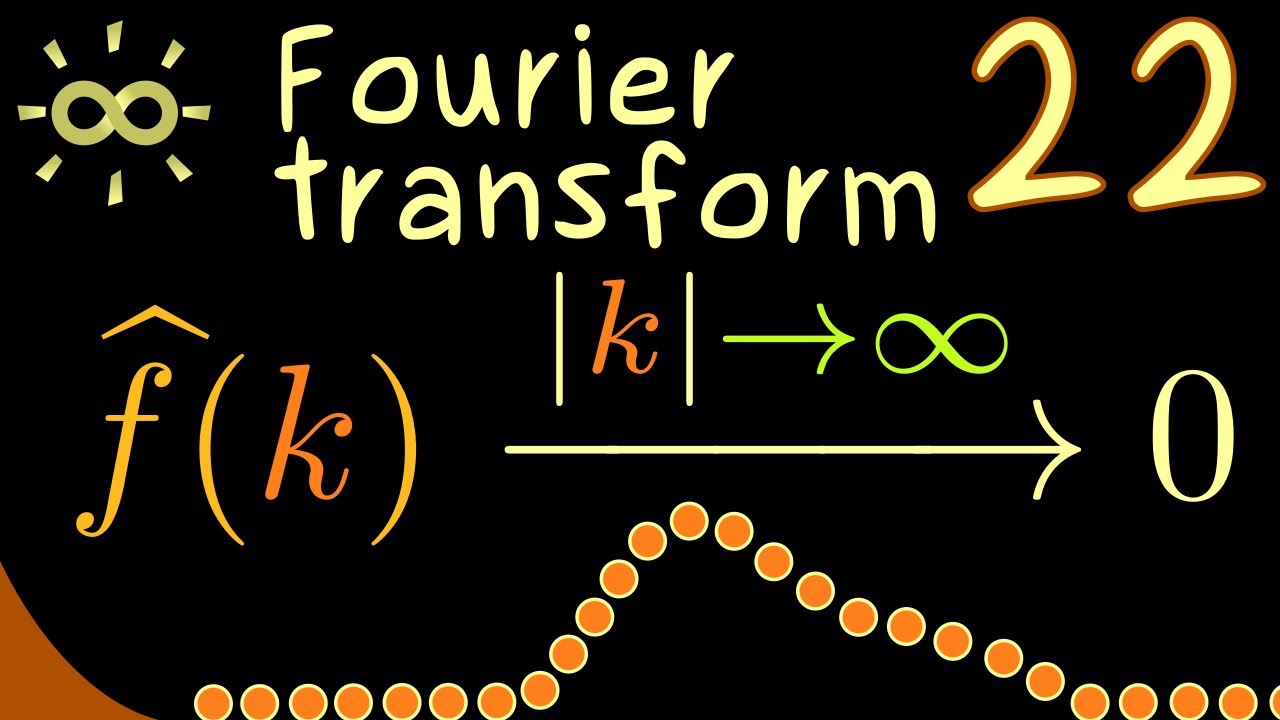
About this video
📝 Find more here: https://tbsom.de/s/ft
👍 Become a member on Steady: https://steadyhq.com/en/brightsideofmaths
👍 Or become a member on Patreon: https://www.patreon.com/bsom
Other possibilities here: https://tbsom.de/sp
You can also support me via PayPal: https://paypal.me/brightmaths
Or via Ko-fi: https://ko-fi.com/thebrightsideofmathematics
Or via Patreon: https://www.patreon.com/bsom
Or via other methods: https://thebrightsideofmathematics.com/support/
Join this channel on YouTube: https://www.youtube.com/channel/UCdwo4k1RQHTcq_-WS7Cazqg/join
💬 Access to the community forum: https://thebrightsideofmathematics.com/community/
🕚 Early access for videos: https://thebrightsideofmathematics.com/early_access/
❓ FAQ: https://thebrightsideofmathematics.com/about/help/
🛠️ What tools do you use: https://thebrightsideofmathematics.com/tools/
📚 Download my books: https://thebrightsideofmathematics.com/books/
🆓 Ad-free access to all videos: https://thebrightsideofmathematics.com/ad-free_access/
▶️ Exclusive supporter videos: https://tbsom.de/s/ft
👏 Your name at the top in the credits of the upcoming videos! (opt-out possible)
📝 PDF versions, quizzes, and Python scripts: https://tbsom.de/s/ft
Please consider to support me if this video was helpful such that I can continue to produce them :)
Each supporter gets access to the additional material. If you need more information, just send me an email: https://tbsom.de/s/mail
Watch the whole video series about Fourier Transform and download PDF versions, quizzes and exercises: https://tbsom.de/s/ft
Supporting me via Steady is the best option for me and you. Please consider choosing a supporter package here: https://tbsom.de/s/subscribe
🌙 There is also a dark mode version of this video: https://youtu.be/xVjDHZ8nnG0
🔆 There is also a bright mode version of this video: https://youtu.be/8PUSH61nAeY
🔆 To find the YouTube-Playlist, click here for the bright version: https://www.youtube.com/playlist?list=PLBh2i93oe2qvtuG8OOg6tZ3FkuCYoHwdf
🌙 And click here for the dark version of the playlist: https://www.youtube.com/playlist?list=PLBh2i93oe2qvd9kFME0SLmiasKbQ7zZSr
🙏 Thanks to all supporters! They are mentioned in the credits of the video :)
This is my video series about Fourier Transform where we talk a lot about Fourier Series. So important topics are trigonometric polynomials, integrable functions, inner products for functions, orthogonal projections, and a lot of formulas for Cosine and Sine functions.I hope that it will help everyone who wants to learn about these things.
#FourierTransform
#Mathematics
#FourierSeries
#Approximation
#LearnMath
#Integrals
#Derivatives
I hope that this helps students, pupils and others. Have fun!
(This explanation fits to lectures for students in their first and second year of study: Mathematics for physicists, Mathematics for the natural science, Mathematics for engineers and so on)
For questions, you can contact me: https://steadyhq.com/en/backend/messages#/me/brightsideofmaths
👍 Become a member on Steady: https://steadyhq.com/en/brightsideofmaths
👍 Or become a member on Patreon: https://www.patreon.com/bsom
Other possibilities here: https://tbsom.de/sp
You can also support me via PayPal: https://paypal.me/brightmaths
Or via Ko-fi: https://ko-fi.com/thebrightsideofmathematics
Or via Patreon: https://www.patreon.com/bsom
Or via other methods: https://thebrightsideofmathematics.com/support/
Join this channel on YouTube: https://www.youtube.com/channel/UCdwo4k1RQHTcq_-WS7Cazqg/join
💬 Access to the community forum: https://thebrightsideofmathematics.com/community/
🕚 Early access for videos: https://thebrightsideofmathematics.com/early_access/
❓ FAQ: https://thebrightsideofmathematics.com/about/help/
🛠️ What tools do you use: https://thebrightsideofmathematics.com/tools/
📚 Download my books: https://thebrightsideofmathematics.com/books/
🆓 Ad-free access to all videos: https://thebrightsideofmathematics.com/ad-free_access/
▶️ Exclusive supporter videos: https://tbsom.de/s/ft
👏 Your name at the top in the credits of the upcoming videos! (opt-out possible)
📝 PDF versions, quizzes, and Python scripts: https://tbsom.de/s/ft
Please consider to support me if this video was helpful such that I can continue to produce them :)
Each supporter gets access to the additional material. If you need more information, just send me an email: https://tbsom.de/s/mail
Watch the whole video series about Fourier Transform and download PDF versions, quizzes and exercises: https://tbsom.de/s/ft
Supporting me via Steady is the best option for me and you. Please consider choosing a supporter package here: https://tbsom.de/s/subscribe
🌙 There is also a dark mode version of this video: https://youtu.be/xVjDHZ8nnG0
🔆 There is also a bright mode version of this video: https://youtu.be/8PUSH61nAeY
🔆 To find the YouTube-Playlist, click here for the bright version: https://www.youtube.com/playlist?list=PLBh2i93oe2qvtuG8OOg6tZ3FkuCYoHwdf
🌙 And click here for the dark version of the playlist: https://www.youtube.com/playlist?list=PLBh2i93oe2qvd9kFME0SLmiasKbQ7zZSr
🙏 Thanks to all supporters! They are mentioned in the credits of the video :)
This is my video series about Fourier Transform where we talk a lot about Fourier Series. So important topics are trigonometric polynomials, integrable functions, inner products for functions, orthogonal projections, and a lot of formulas for Cosine and Sine functions.I hope that it will help everyone who wants to learn about these things.
#FourierTransform
#Mathematics
#FourierSeries
#Approximation
#LearnMath
#Integrals
#Derivatives
I hope that this helps students, pupils and others. Have fun!
(This explanation fits to lectures for students in their first and second year of study: Mathematics for physicists, Mathematics for the natural science, Mathematics for engineers and so on)
For questions, you can contact me: https://steadyhq.com/en/backend/messages#/me/brightsideofmaths
Tags and Topics
Browse our collection to discover more content in these categories.
Video Information
Views
313
Likes
14
Duration
13:03
Published
Nov 3, 2025
Related Trending Topics
LIVE TRENDSRelated trending topics. Click any trend to explore more videos.