Factoring Quadratics Explained by NancyPi
MIT graduate NancyPi demonstrates how to factor quadratic expressions, with a shortcut method available starting at 5:06. Nancy, formerly of MathBFF, explains each step in detail.

NancyPi
2.7M views • May 15, 2018
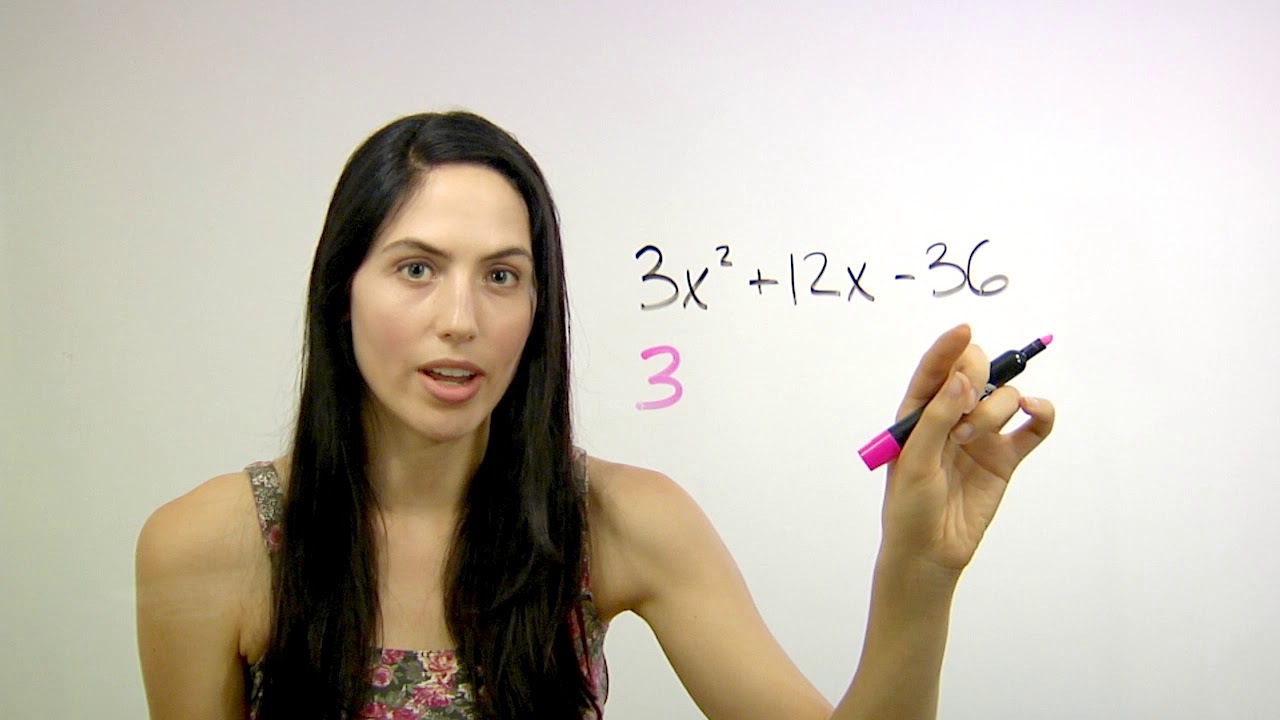
About this video
MIT grad shows how to factor quadratic expressions. If you want to skip to the shortcut method, jump to 5:06. Nancy formerly of MathBFF explains the steps.
Follow Nancy on Instagram: https://instagram.com/nancypi
Twitter: https://twitter.com/nancypi
The shortcut method ("The Magic X") helps you factor any tough quadratic that doesn't begin with x^2 but instead begins with 2x^2 or 3x^2, or 4x^2, etc.
1) IF YOUR QUADRATIC STARTS WITH X^2: It is faster to use the normal method for factoring in this case: trial and error. Say you have x^2 + 4x - 12. You need to find two numbers that multiply to the last number, -12, AND that add to the second coefficient, positive 4. First make a list of all pairs of numbers that multiply to -12. Then check which pair also adds to positive 4. Use the two numbers in this pair to write your factors.
2) IF YOUR QUADRATIC STARTS WITH 2X^2 OR 3X^2 OR 4X^2, ETC:
A) First check whether your leading coefficient (2 or 3 or 4, etc) is just an overall constant that you can factor out of every term in the quadratic. If it is, factor it out first and then use Method #1 above to factor the X^2 expression that remains.
B) If your leading coefficient cannot be factored out evenly from every term, it will be faster and easier to use the shortcut "magic X" method instead of Method #1. See this method explained at time 5:06 in this video.
For how to SOLVE QUADRATIC EQUATIONS by factoring, jump to the video: https://youtu.be/Z5MnP9da4EM
For more of my math videos, check out: http://nancypi.com
Follow Nancy on Instagram: https://instagram.com/nancypi
Twitter: https://twitter.com/nancypi
The shortcut method ("The Magic X") helps you factor any tough quadratic that doesn't begin with x^2 but instead begins with 2x^2 or 3x^2, or 4x^2, etc.
1) IF YOUR QUADRATIC STARTS WITH X^2: It is faster to use the normal method for factoring in this case: trial and error. Say you have x^2 + 4x - 12. You need to find two numbers that multiply to the last number, -12, AND that add to the second coefficient, positive 4. First make a list of all pairs of numbers that multiply to -12. Then check which pair also adds to positive 4. Use the two numbers in this pair to write your factors.
2) IF YOUR QUADRATIC STARTS WITH 2X^2 OR 3X^2 OR 4X^2, ETC:
A) First check whether your leading coefficient (2 or 3 or 4, etc) is just an overall constant that you can factor out of every term in the quadratic. If it is, factor it out first and then use Method #1 above to factor the X^2 expression that remains.
B) If your leading coefficient cannot be factored out evenly from every term, it will be faster and easier to use the shortcut "magic X" method instead of Method #1. See this method explained at time 5:06 in this video.
For how to SOLVE QUADRATIC EQUATIONS by factoring, jump to the video: https://youtu.be/Z5MnP9da4EM
For more of my math videos, check out: http://nancypi.com
Tags and Topics
Browse our collection to discover more content in these categories.
Video Information
Views
2.7M
Likes
73.4K
Duration
9:14
Published
May 15, 2018
User Reviews
4.8
(540) Related Trending Topics
LIVE TRENDSRelated trending topics. Click any trend to explore more videos.