Extended Euclidean Algorithm for Computing Bézout Coefficients
This article explains how the Extended Euclidean Algorithm can be used to find Bézout coefficients, which express the greatest common divisor of two integers as a linear combination of those integers, based on Bézout's lemma.

Existsforall Academy
699 views • Sep 4, 2021
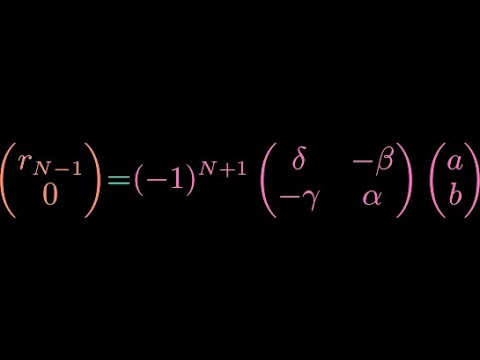
About this video
Bézout's lemma tells us that the greatest common divisor of two integers can be written as an integer linear combination of the two integers. The question then arises as to how we can determine the two coefficients. This is where the extended Euclidean algorithm comes into play. Amazingly, it turns out that we can use the sequence of quotients and remainders from the Euclidean algorithm to produce the coefficients. This is usually expressed as an algorithm involving substitutions into equations, but we have preferred to express the idea as a neat formula involving matrix multiplication and the determinant.
Like, subscribe, and share! To find out more about us:
- Visit https://existsforall.com to check out our services
- Get our Rigorous Elementary Mathematics books on Amazon: https://www.amazon.com/dp/B0DGDNK6TM?binding=paperback
Copyright © Existsforall Academy Inc. All rights reserved.
Like, subscribe, and share! To find out more about us:
- Visit https://existsforall.com to check out our services
- Get our Rigorous Elementary Mathematics books on Amazon: https://www.amazon.com/dp/B0DGDNK6TM?binding=paperback
Copyright © Existsforall Academy Inc. All rights reserved.
Tags and Topics
Browse our collection to discover more content in these categories.
Video Information
Views
699
Likes
9
Duration
11:41
Published
Sep 4, 2021
Related Trending Topics
LIVE TRENDSRelated trending topics. Click any trend to explore more videos.
Trending Now