Exploring Turing Machines, Quantum Entanglement, and Operator Algebras 🔍

Henry Yuen (University of Toronto)
Richard M. Karp Distinguished Lecture Series, Spring 2020
https://simons.berkeley.edu/events/rmklectures2020-spring-3

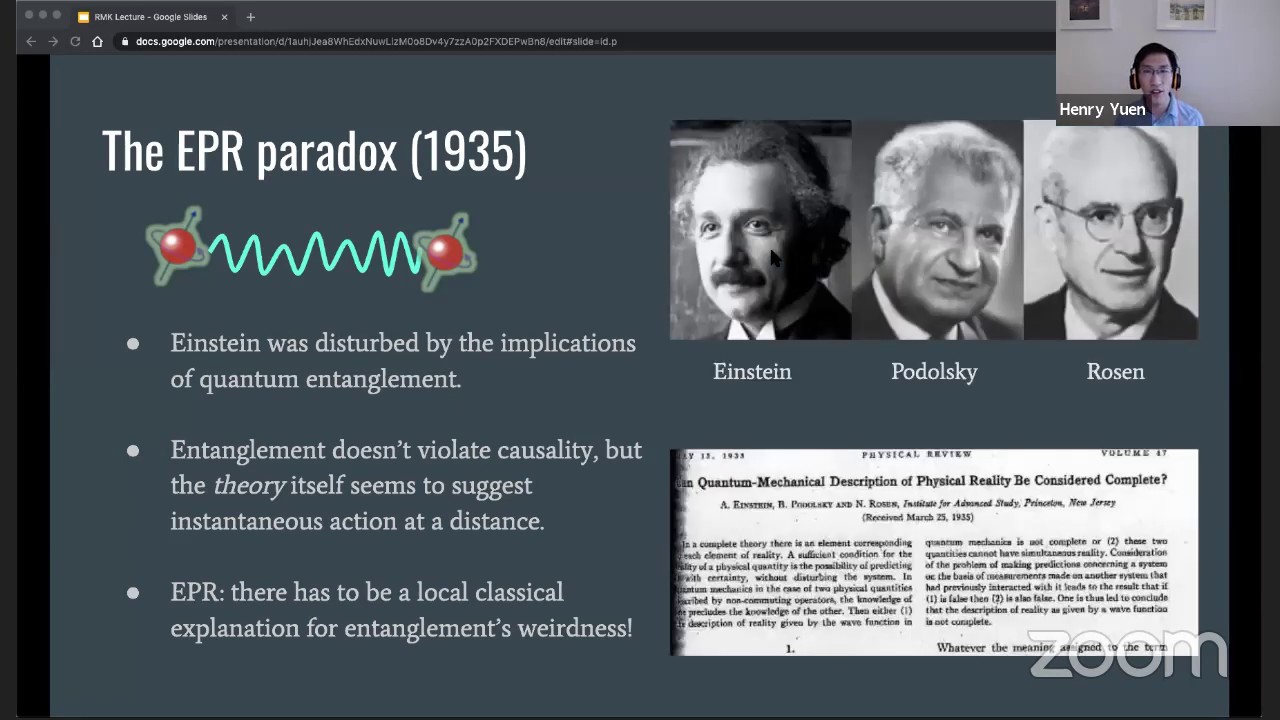
In a recent result known as "MIP* = RE," ideas from three disparate fields of study — computational complexity theory, quantum information, and operator algebras — have come together to simultaneously resolve long-standing open problems in each field, including a 44-year old mystery in mathematics known as Connes’ Embedding Problem. In this talk, I will describe the evolution and convergence of ideas behind MIP* = RE: it starts with three landmark discoveries from the 1930s (Turing’s notion of a universal computing machine, the phenomenon of quantum entanglement, and von Neumann’s theory of operators), and ends with some of the most cutting-edge developments from theoretical computer science and quantum computing.

This talk is aimed at a general scientific audience, and will not assume any specialized background in complexity theory, quantum physics, or operator algebras.