Exploring Paillier Homomorphic Encryption & Share Conversion Protocols 🔐

Seminario di De Cifris Athesis, in collaborazione con il Laboratorio di Matematica Industriale e Crittografia dell'Università degli Studi di Trento (CryptoLabTN) e la Fondazione Bruno Kessler (FBK). Abstract: In this seminar we will talk about one of the public-key cryptosystems introduced by Pascal Paillier. We will start defining what is a n-th residuosity class and presenting the Composite Residuosity and the Composite Residuosity Class problems. We will see how these two problems are related with the milestone problems of the public key cryptography: factorization and root extraction. Then we will describe the encryption/decryption scheme and briefly discuss its correctness, security and complexity. 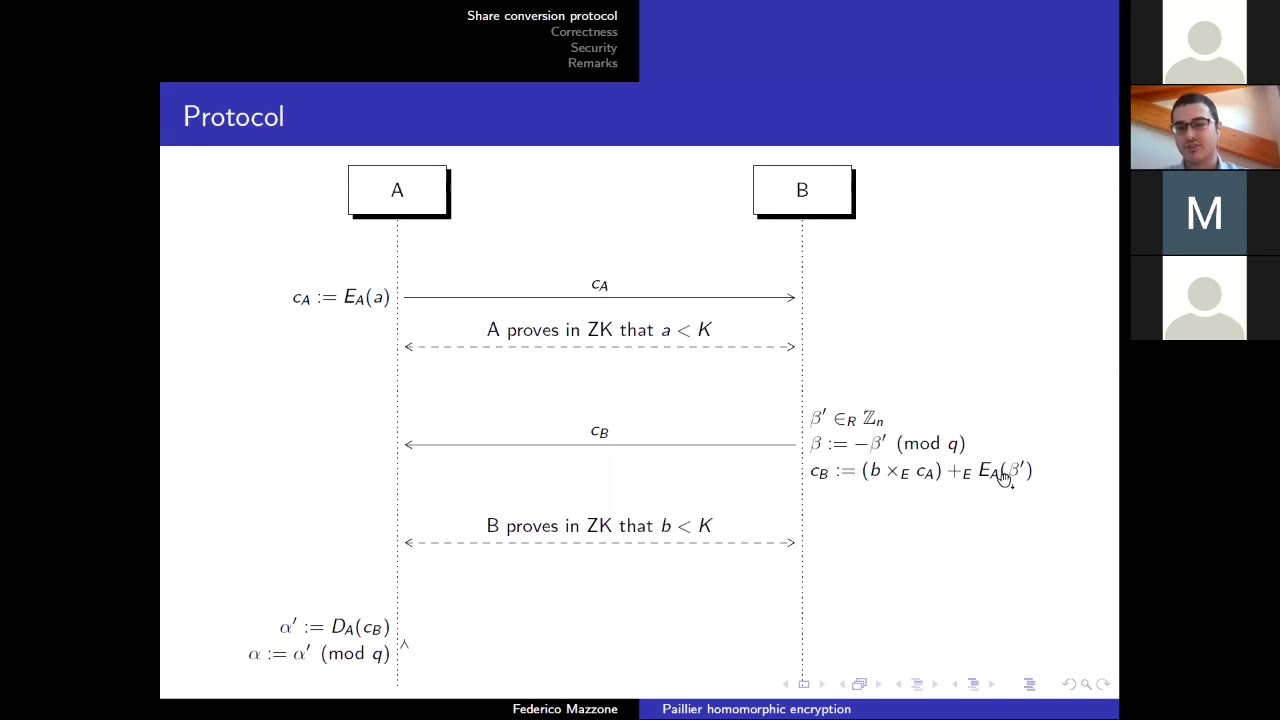Finally, we will prove the homomorphic properties of this cryptosystem and we will show how to exploit them in order to create a multiplicative-to-additive share conversion protocol. Website: De Cifris Athesis: https://www.decifris.it/seminarilocali/decifrisathesis.html De Componendis Cifris: https://www.decifris.it