Enhanced Analysis of Discrete Gaussian & Subgaussian Distributions in Lattice Cryptography 🔐

Nicholas Genise (UC San Diego)
Lattices: Algorithms, Complexity, and Cryptography
Seminar, Apr. 7, 2020

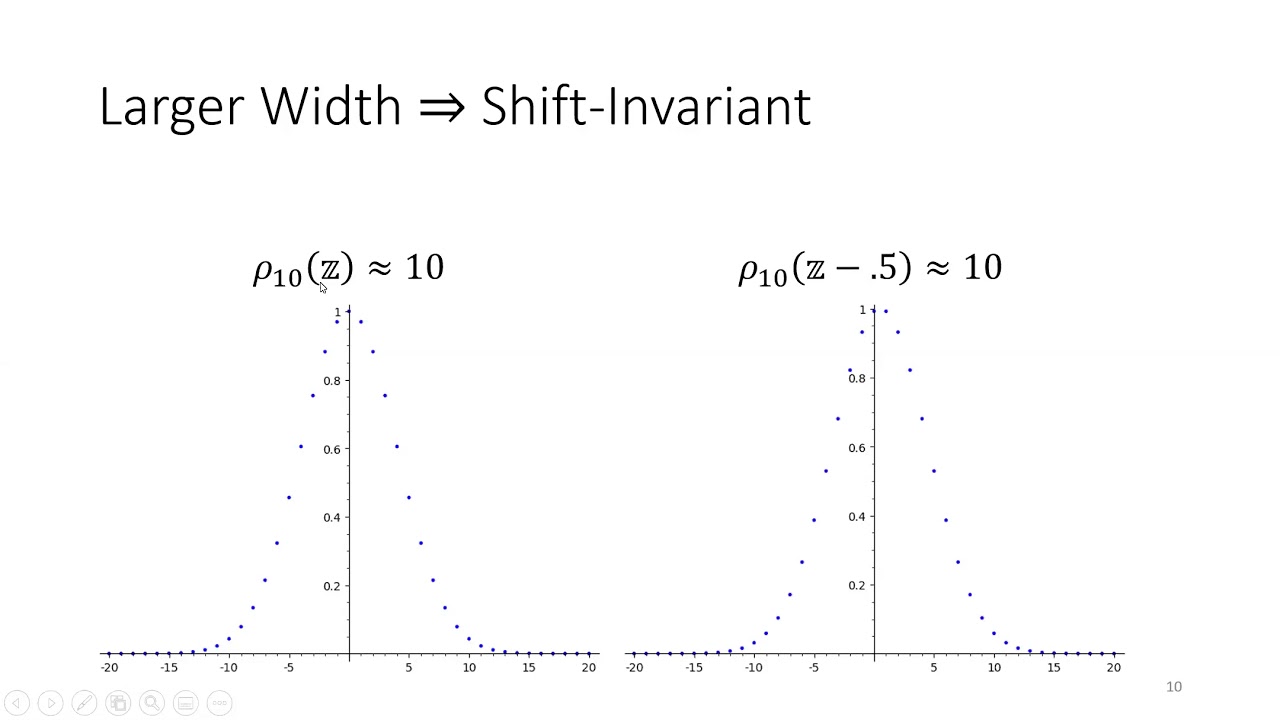
Discrete Gaussian distributions over lattices are central to lattice-based cryptography, and to the computational and mathematical aspects of lattices more broadly. The literature contains a wealth of useful theorems about the behavior of discrete Gaussians under convolutions and related operations. Yet despite their structural similarities, most of these theorems are formally incomparable, and their proofs tend to be monolithic and written nearly “from scratch,” making them unnecessarily hard to verify, understand, and extend.

In this work we present a modular framework for analyzing linear operations on discrete Gaussian distributions. The framework abstracts away the particulars of Gaussians, and usually reduces proofs to the choice of appropriate linear transformations and elementary linear algebra. To showcase the approach, we establish several general properties of discrete Gaussians, and show how to obtain all prior convolution theorems (along with some new ones) as straightforward corollaries. As another application, we describe a self-reduction for Learning With Errors (LWE) that uses a fixed number of samples to generate an unlimited number of additional ones (having somewhat larger error). The distinguishing features of our reduction are its simple analysis in our framework, and its exclusive use of discrete Gaussians without any loss in parameters relative to a prior mixed discrete-and-continuous approach.

As a contribution of independent interest, for subgaussian random matrices we prove a singular value concentration bound with explicitly stated constants, and we give tighter heuristics for specific distributions that are commonly used for generating lattice trapdoors. These bounds yield improvements in the concrete bit-security estimates for trapdoor lattice cryptosystems.

This is joint work with Daniele Micciancio, Chris Peikert, and Michael Walter.