Efficient Java Code for Calculating GCD Using Euclid's Algorithm 🔢

This is the code for the Euclid's Algorithm to find the GCD (Greatest Common Divisor) of two numbers. The code is written in Java. There are three variations shown here:
1) Recursive GCD
2) Iterative GCD
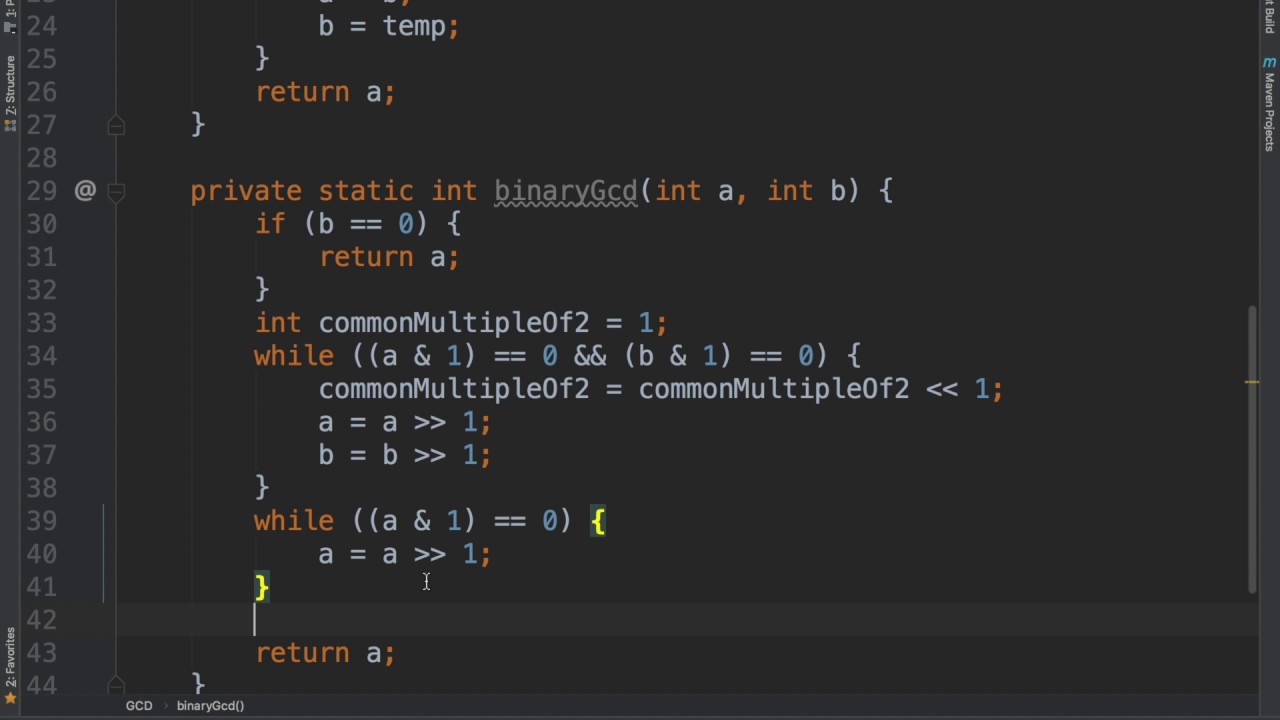
3) Binary GCD

The GCD of two given numbers is defined as the largest possible number which divides both the numbers with no remainder. The GCD of a number is also sometimes called Highest Common Factor.

Do check out the other two videos on the proof of the algorithm (https://youtu.be/B5HKW99AvV0) and an exciting question (https://youtu.be/D-DYtUmRMa4)!

Code:
https://github.com/gkcs/Competitive-Programming/blob/master/src/main/java/main/java/videos/GCD.java
Codechef Problem:
https://www.codechef.com/problems/GCDQ
References:
https://brilliant.org/wiki/greatest-common-divisor/
https://www.khanacademy.org/computing/computer-science/cryptography/modarithmetic/a/the-euclidean-algorithm
https://ocw.mit.edu/courses/electrical-engineering-and-computer-science/6-042j-mathematics-for-computer-science-fall-2010/readings/MIT6_042JF10_chap04.pdf