Discover Willans' Exact Formula for Prime Numbers 🔢

Thanks to my supporters on Patreon! Get early access to videos and more: https://www.patreon.com/EricRowland

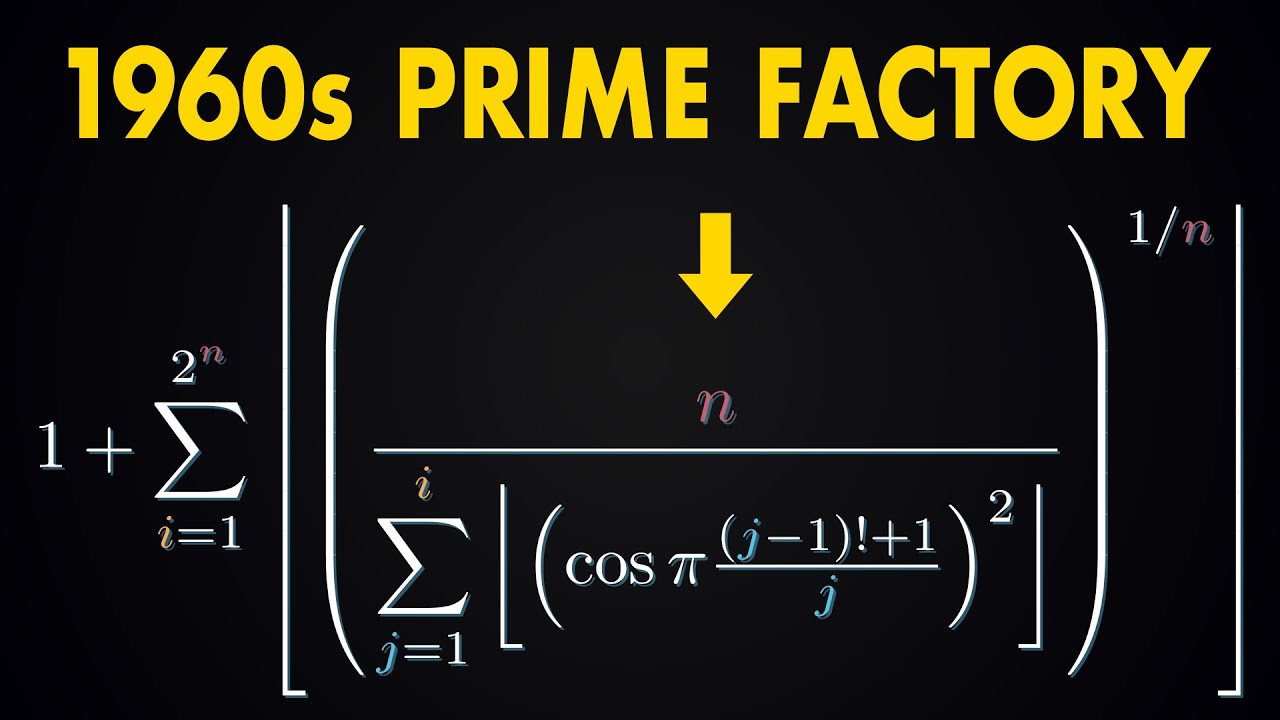
Formulas for the nth prime number actually exist! One was cleverly engineered in 1964 by C. P. Willans. But is it useful?

----------------

References:

Herbert Wilf, What is an answer?, The American Mathematical Monthly 89 (1982) 289–292.
https://doi.org/10.1080/00029890.1982.11995435

C. P. Willans, On formulae for the nth prime number, The Mathematical Gazette 48 (1964) 413–415.
https://doi.org/10.2307/3611701

Further reading:

Jeffrey Shallit, No formula for the prime numbers?.
http://recursed.blogspot.com/2013/01/no-formula-for-prime-numbers.html

----------------

# Python code

import math

def prime(n):
return 1 + sum([
math.floor(pow(n/sum([
math.floor(pow(math.cos(math.pi * (math.factorial(j - 1) + 1)/j), 2))
for j in range(1, i+1)
]), 1/n))
for i in range(1, pow(2, n)+1)
])

----------------

(* Mathematica code *)

prime[n_] := 1 + Sum[Floor[(n/Sum[Floor[Cos[Pi ((j - 1)! + 1)/j]^2], {j, 1, i}])^(1/n)], {i, 1, 2^n}]

----------------

0:00 A formula for primes?
1:24 Engineering a prime detector
4:00 Improving the prime detector
5:46 Counting primes
6:29 Determining the nth prime
9:42 The final step
11:36 What counts as a formula?
12:56 What's the point?
13:51 Who was Willans?

----------------

Animated with Manim. https://www.manim.community
Thanks to Ken Emmer for supplying the microphone.

Web site: https://ericrowland.github.io