Directed Hamiltonian Path is NP-Complete via 3SAT Reduction

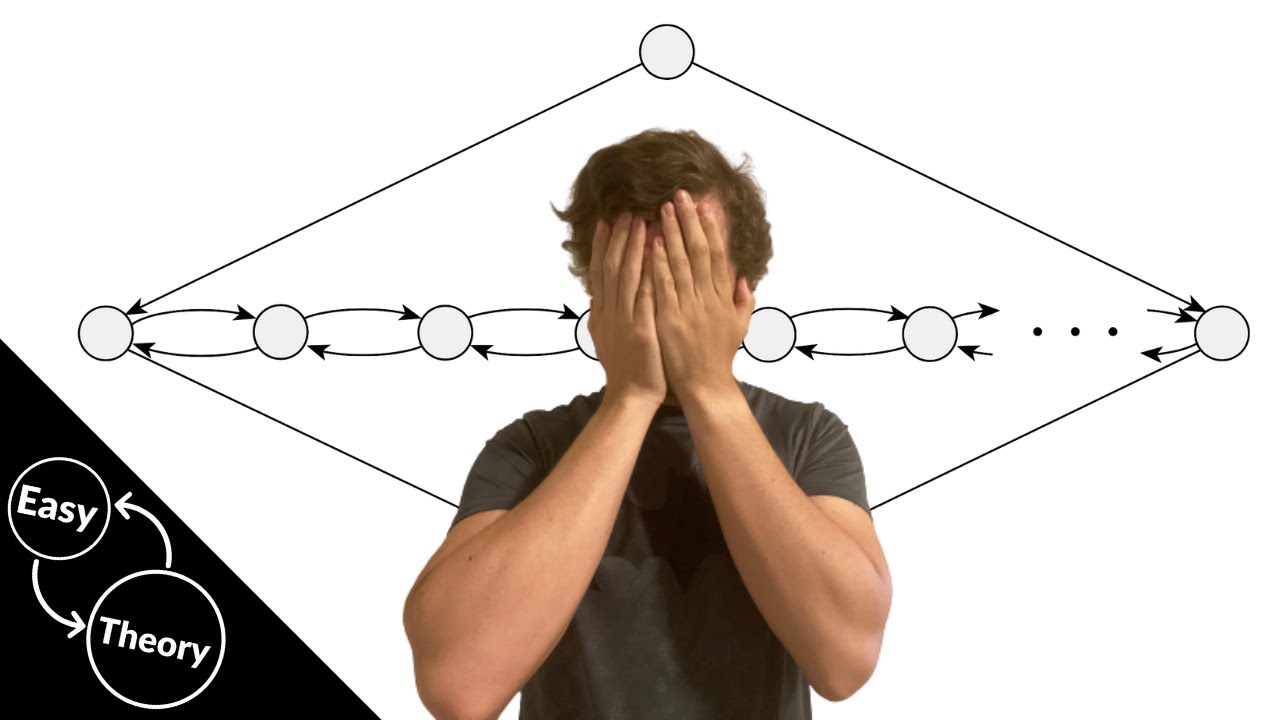
Here we show that the directed hamiltonian path problem is NP-complete by showing it is in NP and is NP-hard via a polynomial-time reduction from the 3SAT problem. The key in the reduction is to embed the variables and clauses of the formula as "gadgets" and connect them up in a useful way. Each of the possible "paths" through the variable gadgets corresponds to a variable assignment.

(The thumbnail background comes courtesy of the Sipser textbook)

Easy Theory Website: https://www.easytheory.org
GoFundMe: https://www.gofundme.com/f/easy-theory-video-studio
Patreon: https://www.patreon.com/EasyTheoryYT
Fourthwall: https://easy-theory-llc-shop.fourthwall.com
Problem Solving channel: ​⁠ @easytheoryprobsolve

If you like this content, please consider subscribing to my channel: https://www.youtube.com/channel/UC3VY6RTXegnoSD_q446oBdg?sub_confirmation=1