Mastering Matrix Diagonalization: Simplify 2x2 Matrices in Engineering Math 📊
Learn how to diagonalize 2x2 matrices with step-by-step methods. Enhance your engineering mathematics skills and understand the importance of diagonalization in simplifying complex problems.

Mathspedia
9.3K views • Jan 1, 2024
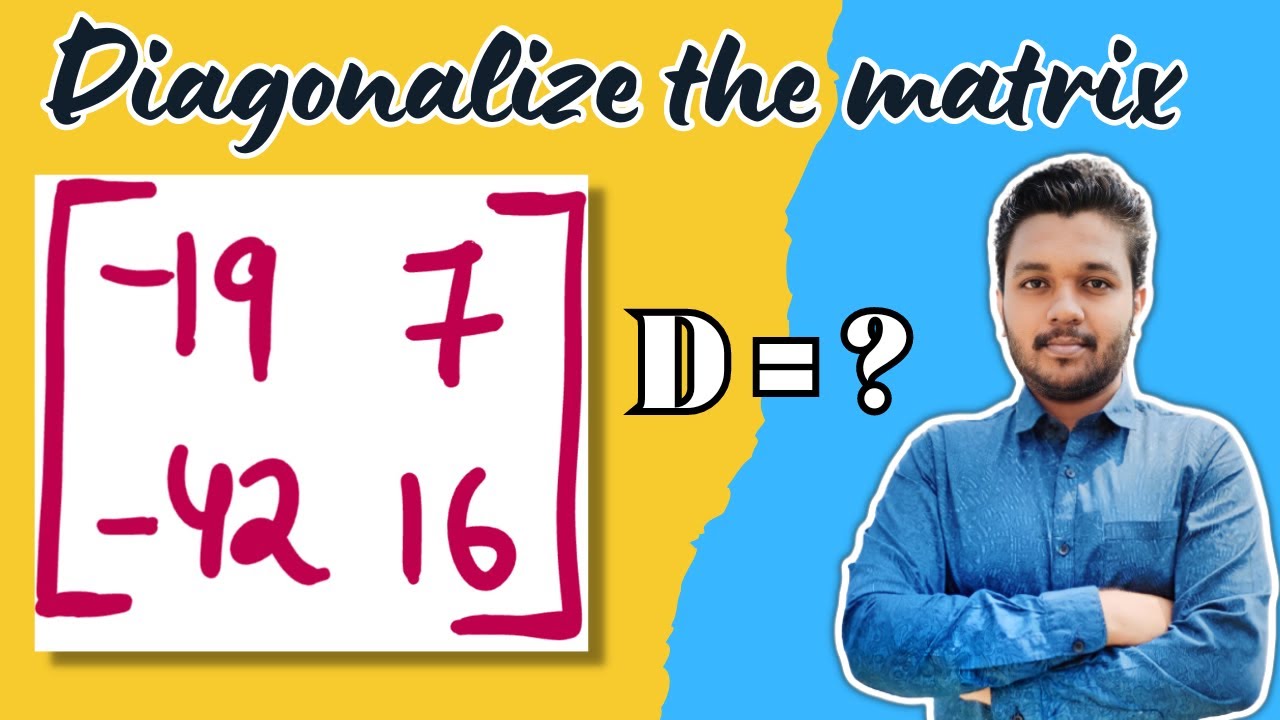
About this video
Diagonalization is a process by which a square matrix ( A ) is transformed into a diagonal matrix ( D ) through a similarity transformation involving an invertible matrix ( P ). The diagonal matrix ( D ) has the eigenvalues of ( A ) on its main diagonal, and ( P ) is composed of the corresponding eigenvectors.
The general formula for diagonalization is given by:
D = P^{-1} A P
Here, ( D ) is the diagonal matrix, and ( P ) is the matrix composed of the eigenvectors of ( A ).
1.Find Eigenvalues: - Solve the characteristic equation to find the eigenvalues.
2. Find Eigenvectors: - For each eigenvalue , find the corresponding eigenvector by solving the system.
3. Form Matrix P:- Arrange the eigenvectors as columns to form the matrix ( P ).
4. Form Diagonal Matrix D: - The diagonal matrix ( D ) is formed using the eigenvalues on the main diagonal.
It's important to note that not all matrices are diagonalizable. A matrix is diagonalizable if and only if it has ( n ) linearly independent eigenvectors, where ( n ) is the size of the matrix.
---------------------------------------------------------------------------------------------------------------------------
Welcome guys ✌
For any queries DM 👇
https://www.instagram.com/abhijithambady_/
SUBSCRIBE 👇
https://www.youtube.com/c/MATHSPEDIAabhi?sub_confirmation=1
🔊IF YOU UNDERSTOOD THE CONCEPT DO GIVE ONE LIKE👍
🔊IF YOU HAVE ANY CLARIFICATION ABOUT THE CONCEPT
PLEASE DO COMMENT💬
🔊IF YOU WANT MORE VIDEOS IN FUTURE DO SUBSCRIBE🙏
🔊IF YOU ARE FED UP WITH THE NOTIFICATION ALERT NO NEED TO PRESS 🔔 OR OTHERWISE DO PRESS 🔔
AND ONE MORE THING THANKS FOR WATCHING VIDEO🙏
--------------------------------------------------------------------------------------------------------------------------
#mathspedia #diagonalisethematrix #engineeringmathematics #eigenvalue #eigenvector #diagonlisation
The general formula for diagonalization is given by:
D = P^{-1} A P
Here, ( D ) is the diagonal matrix, and ( P ) is the matrix composed of the eigenvectors of ( A ).
1.Find Eigenvalues: - Solve the characteristic equation to find the eigenvalues.
2. Find Eigenvectors: - For each eigenvalue , find the corresponding eigenvector by solving the system.
3. Form Matrix P:- Arrange the eigenvectors as columns to form the matrix ( P ).
4. Form Diagonal Matrix D: - The diagonal matrix ( D ) is formed using the eigenvalues on the main diagonal.
It's important to note that not all matrices are diagonalizable. A matrix is diagonalizable if and only if it has ( n ) linearly independent eigenvectors, where ( n ) is the size of the matrix.
---------------------------------------------------------------------------------------------------------------------------
Welcome guys ✌
For any queries DM 👇
https://www.instagram.com/abhijithambady_/
SUBSCRIBE 👇
https://www.youtube.com/c/MATHSPEDIAabhi?sub_confirmation=1
🔊IF YOU UNDERSTOOD THE CONCEPT DO GIVE ONE LIKE👍
🔊IF YOU HAVE ANY CLARIFICATION ABOUT THE CONCEPT
PLEASE DO COMMENT💬
🔊IF YOU WANT MORE VIDEOS IN FUTURE DO SUBSCRIBE🙏
🔊IF YOU ARE FED UP WITH THE NOTIFICATION ALERT NO NEED TO PRESS 🔔 OR OTHERWISE DO PRESS 🔔
AND ONE MORE THING THANKS FOR WATCHING VIDEO🙏
--------------------------------------------------------------------------------------------------------------------------
#mathspedia #diagonalisethematrix #engineeringmathematics #eigenvalue #eigenvector #diagonlisation
Tags and Topics
Browse our collection to discover more content in these categories.
Video Information
Views
9.3K
Likes
136
Duration
20:44
Published
Jan 1, 2024
User Reviews
4.5
(1) Related Trending Topics
LIVE TRENDSRelated trending topics. Click any trend to explore more videos.
Trending Now