Algorithmic Analysis: Understanding Asymptotic Complexity

Título: Algorithmic Analysis: Asymptotic Complexity

Descripción: In this video Big O notation is explained as a way to describe the complexity of an algorithm by estimating the time required to complete it based on the size of the input. The worst-case and best-case scenarios are discussed, with the goal of guaranteeing that every solution falls within certain bounds.

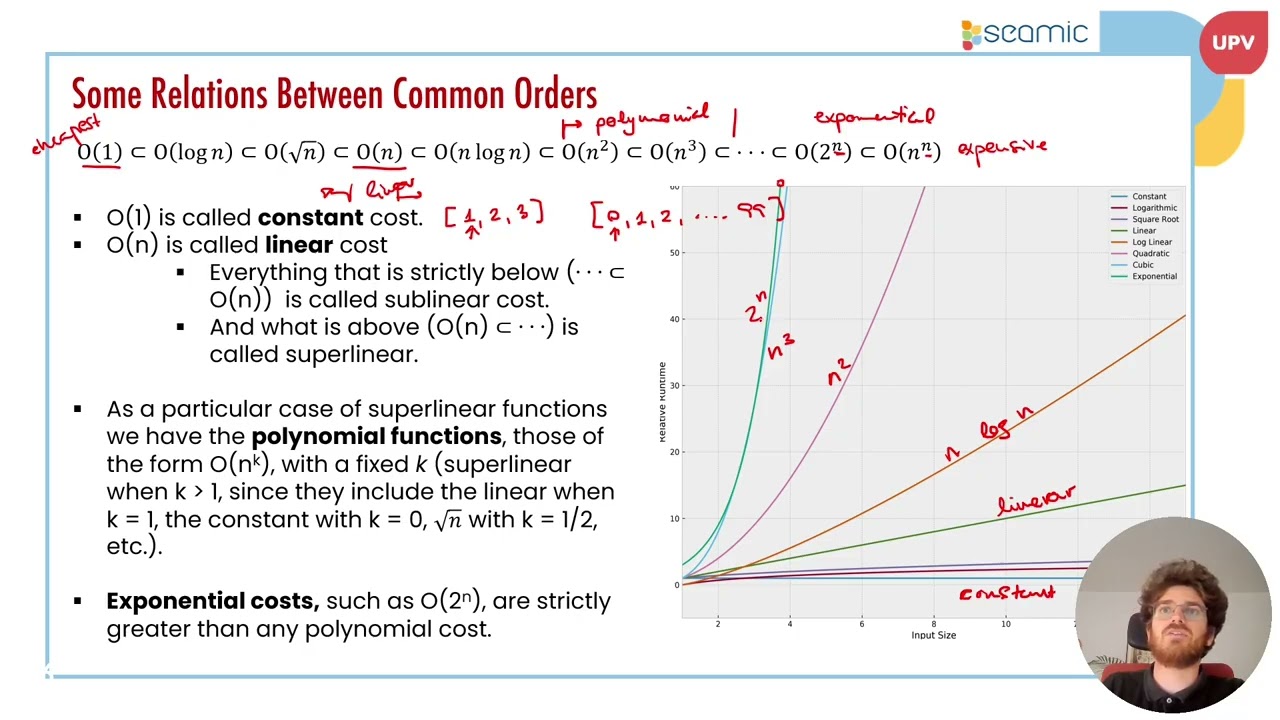
Different types of functions are introduced, including constant, linear, polynomial, and exponential, which can be used to describe the complexity of an algorithm. Examples are provided, along with a graph illustrating the growth rates of each type.

Properties of Big O notation are also discussed, such as how to combine the costs of different instructions and how to handle loops and conditional statements. The importance of focusing on the most significant term in an expression is emphasized.


Autor/a: GALINDO JIMENEZ CARLOS SANTIAGO

Curso: Este vídeo es el 27/34 del curso SEAMIC Computer Science II. https://www.youtube.com/playlist?list=PL6kQim6ljTJtqJz2Qe0_6jAtLVluSFR5b
Curso: Este vídeo es el 88/120 del curso SEAMIC (Bachelor's Degree in Systems Engineering and Management for Innovation Challenges). https://www.youtube.com/playlist?list=PL6kQim6ljTJtWBXvKMuuaHPdgj4VcN6IH


+ Universitat Politècnica de València UPV: https://www.upv.es
+ Más vídeos en: https://www.youtube.com/valenciaupv
+ Accede a nuestros MOOC: https://upvx.es

#big o notation #asymptotic complexity #theoretical computer science #algorithmic analysis #seamic #CS2