Quantum Info Theory: Fall 2020 Lecture 3 📘

These are recordings of 12 lectures I gave for a graduate class at the University of Toronto, centered on advanced topics in quantum information theory. Lectures can be found on the course homepage at: http://henryyuen.net/classes/fall2020/

The goal of the course is to take a deep dive into some of the most exciting topics at the frontier of quantum complexity theory and quantum cryptography. There have been very exciting developments recently, including the connection between the complexity of quantum multiprover interactive proofs and questions in functional analysis and operator algebras; new cryptographic primitives such as quantum money/quantum copy-protection; quantum homomorphic encryption and the use of lattice cryptography; the quantum PCP Conjecture and its connections with condensed matter physics. This course will cover advanced and cutting edge topics in quantum information theory, organized into the following two themes:

Classical verification of quantum systems: nonlocal games, self-testing, verifiable delegation of quantum computation, the use of lattice cryptography, and MIP* = RE and its connection to the Connes’ Embedding Conjecture.

Hamiltonian complexity theory: QMA completeness, local Hamiltonians, QMA(2), Quantum PCP Conjecture, area laws, and algorithms for solving local Hamiltonians.

----------------

Lecture schedule:

Lecture 1 - quantum information theory refresher, Bell's theorem and the CHSH game.
Lecture 2 - Introduction to Hamiltonian Complexity.
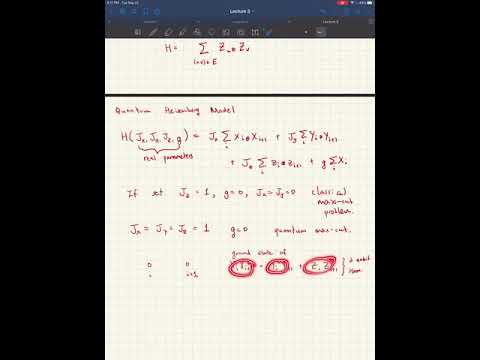
Lecture 3 - QMA completeness.
Lecture 4 - Finish up QMA completeness, classical PCP Theorem.
Lecture 5 - Quantum PCP Conjecture.
Lecture 6 - Complexity of quantum states, and no-go theorems for Quantum PCP.
Lecture 7 - Rigidity of the CHSH game.
Lecture 8 - Two-prover protocols for verifying quantum computations.
Lecture 9 - MIP* = RE, part I
Lecture 10 - MIP* = RE, part II
Lecture 11 - MIP* = RE, part III
Lecture 12 - The power of unentanglement and QMA(2)